
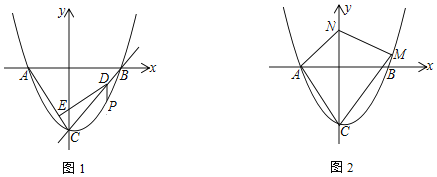
【题目】如图1,平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴于A、B两点
交x轴于A、B两点![]() 在B的左边
在B的左边![]() ,交y轴于C,直线
,交y轴于C,直线![]() 经过B、C两点.
经过B、C两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 为直线BC下方的抛物线上一点,
为直线BC下方的抛物线上一点,![]() 轴交BC于D点,过D作
轴交BC于D点,过D作![]() 于E点
于E点![]() 设
设![]() ,求m的最大值及此时P点坐标;
,求m的最大值及此时P点坐标;
![]() 探究是否存在第一象限的抛物线上一点M,以及y轴正半轴上一点N,使得
探究是否存在第一象限的抛物线上一点M,以及y轴正半轴上一点N,使得![]() ,且
,且![]() 若存在,求出M、N两点坐标;否则,说明理由.
若存在,求出M、N两点坐标;否则,说明理由.
【答案】![]() ;
;![]() m的最大值为
m的最大值为![]() ,此时点P的坐标为
,此时点P的坐标为![]() ;
;![]() 存在满足条件的M、N两点,坐标分别为
存在满足条件的M、N两点,坐标分别为![]() 、
、![]()
【解析】
![]() 利用直线
利用直线![]() 经过B、C两点,先求出点B、C的坐标,然后利用待定系数法求出抛物线的解析式;
经过B、C两点,先求出点B、C的坐标,然后利用待定系数法求出抛物线的解析式;![]() 根据表达式
根据表达式![]() ,设出D点坐标
,设出D点坐标![]() ,用含a的代数式分别表达出线段PD、DE,转化成m关于a的二次函数,再求m的最大值及P点坐标;
,用含a的代数式分别表达出线段PD、DE,转化成m关于a的二次函数,再求m的最大值及P点坐标;![]() 根据条件
根据条件![]() ,且
,且![]() ,利用三角形的全等去确定满足条件的M、N点,再根据函数解析式去它们的坐标.
,利用三角形的全等去确定满足条件的M、N点,再根据函数解析式去它们的坐标.
![]() 直线
直线![]() 经过坐标轴上B、C两点,
经过坐标轴上B、C两点,
![]() ,
,![]()
而B、C两点在抛物线![]() 上,于是有
上,于是有![]()
解得![]() ,
,![]()
故抛物线的解析式为![]() .
.
![]() 连接AD,并延长PD交x轴于H点
连接AD,并延长PD交x轴于H点![]() 如图
如图![]() ,设H点坐标为
,设H点坐标为![]() ,则D点坐标为
,则D点坐标为![]() ,P点坐标为
,P点坐标为![]() ,所以
,所以![]() ,
,![]()

由![]() ,当
,当![]() 时,解得
时,解得![]() 或4,于是可知
或4,于是可知![]() ,
,![]() 且
且![]()
![]() ,
,![]()
由于![]()
于是有![]()
即:![]()
得![]()
即:当![]() 时,m的最大值为
时,m的最大值为![]()
此时![]() 可代入
可代入![]() 得
得![]()
故m的最大值为![]() ,此时点P的坐标为
,此时点P的坐标为![]()
![]() 过N点分别作
过N点分别作![]() 交CA延长线于E点,作
交CA延长线于E点,作![]() 于F点,如图2
于F点,如图2

![]() ,
,
而在四边形NECF中,![]() ,
,![]() ,
,![]() ,
,![]()
又![]() ,且
,且![]()
![]() ≌
≌![]() ,
,![]()
![]() 平分
平分![]()
若设CM与X轴交点为G点,根据轴对称,可知G点坐标为![]()
由![]() 、
、![]() 两点可得
两点可得![]() :
:![]()
而点M是直线CM与抛物线的交点,于是有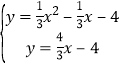
解得![]() ,
,![]() 或
或![]() ,
,![]()
由此可知点M的坐标为![]()
设N点坐标为![]() ,根据
,根据![]()
解得![]() ,所以N点坐标为
,所以N点坐标为![]()
故存在满足条件的M、N两点,坐标分别为![]() 、
、![]()


科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
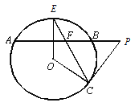
【题目】如图,AB 是⊙O 的弦,半径OE⊥ AB ,P 为 AB 的延长线上一点,PC 与⊙O相切于点 C,连结 CE,交 AB 于点 F,连结 OC.
(1)求证:PC=PF.
(2)连接 BE,若∠CEB=30°,半径为 8,tan P ![]() ,求 FB 的长.
,求 FB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:ABCP=BDCD;
(3)当AB=5cm,AC=12cm时,求线段PC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
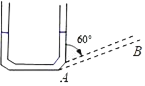
A. 4cmB. 2![]() cmC. 3cmD. 8cm
cmC. 3cmD. 8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若|m+3|+![]() =0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
=0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
A. y=![]() (x﹣3)2+2B. y=
(x﹣3)2+2B. y=![]() (x+3)2﹣2
(x+3)2﹣2
C. y=![]() (x﹣3)2﹣2D. y=
(x﹣3)2﹣2D. y=![]() (x+3)2+2
(x+3)2+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com