
ЁОЬтФПЁПШчЭМЃЌ![]() жа,ЁЯC=90Ёу,
жа,ЁЯC=90Ёу,![]() ,
,![]() ,ШєЖЏЕуPДгЕуCПЊЪМ,АД
,ШєЖЏЕуPДгЕуCПЊЪМ,АД![]() ЕФТЗОЖдЫЖЏ,ЧвЫйЖШЮЊУПУы1cm,ЩшГіЗЂЕФЪБМфЮЊtУыЃЎ
ЕФТЗОЖдЫЖЏ,ЧвЫйЖШЮЊУПУы1cm,ЩшГіЗЂЕФЪБМфЮЊtУыЃЎ
![]() ЕуPГіЗЂ2УыКѓ,ЧѓCPКЭBPЕФГЄЃЎ
ЕуPГіЗЂ2УыКѓ,ЧѓCPКЭBPЕФГЄЃЎ
![]() ЮЪtТњзуЪВУДЬѕМўЪБ
ЮЪtТњзуЪВУДЬѕМўЪБ![]() ЕФжЕЛђШЁжЕЗЖЮЇ
ЕФжЕЛђШЁжЕЗЖЮЇ![]() ,
,![]() ЮЊжБНЧШ§НЧаЮЃП
ЮЊжБНЧШ§НЧаЮЃП
![]() СэгавЛЕуQ,ДгЕуCПЊЪМ,АД
СэгавЛЕуQ,ДгЕуCПЊЪМ,АД![]() ЕФТЗОЖдЫЖЏ,ЧвЫйЖШЮЊУПУы2cm,ШєPЁЂQСНЕуЭЌЪБГіЗЂ,ЕБPЁЂQжагавЛЕуЕНДяжеЕуЪБ,СэвЛЕувВЭЃжЙдЫЖЏ
ЕФТЗОЖдЫЖЏ,ЧвЫйЖШЮЊУПУы2cm,ШєPЁЂQСНЕуЭЌЪБГіЗЂ,ЕБPЁЂQжагавЛЕуЕНДяжеЕуЪБ,СэвЛЕувВЭЃжЙдЫЖЏ![]() ЕБtЮЊКЮжЕЪБ,жБЯпPQАб
ЕБtЮЊКЮжЕЪБ,жБЯпPQАб![]() ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗжЃП
ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗжЃП
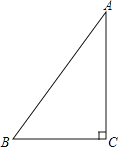
ЁОД№АИЁП(1)PB=![]() cmЃЛCP=2cmЃЛ(2)
cmЃЛCP=2cmЃЛ(2)![]() Лђ
Лђ![]() ЃЛ(3)
ЃЛ(3)![]() Лђ6Уы.
Лђ6Уы.
ЁОНтЮіЁП
![]() ЪзЯШРћгУЙДЙЩЖЈРэМЦЫуГіACГЄ,ИљОнЬтвтПЩЕУ
ЪзЯШРћгУЙДЙЩЖЈРэМЦЫуГіACГЄ,ИљОнЬтвтПЩЕУ![]() ,дйРћгУЙДЙЩЖЈРэМЦЫуГіPBЕФГЄ,НјЖјПЩЕУ
,дйРћгУЙДЙЩЖЈРэМЦЫуГіPBЕФГЄ,НјЖјПЩЕУ![]() ЕФжмГЄЃЛ
ЕФжмГЄЃЛ
![]() ЕБPдкACЩЯдЫЖЏЪБ
ЕБPдкACЩЯдЫЖЏЪБ![]() ЮЊжБНЧШ§НЧаЮ,гЩДЫПЩЕУ
ЮЊжБНЧШ§НЧаЮ,гЩДЫПЩЕУ![]() ЃЛЕБPдкABЩЯЪБ,
ЃЛЕБPдкABЩЯЪБ,![]() ЪБ,
ЪБ,![]() ЮЊжБНЧШ§НЧаЮ,ЪзЯШМЦЫуГіCPЕФГЄ,ШЛКѓдйРћгУЙДЙЩЖЈРэМЦЫуГіAPГЄ,НјЖјПЩЕУД№АИЃЎ
ЮЊжБНЧШ§НЧаЮ,ЪзЯШМЦЫуГіCPЕФГЄ,ШЛКѓдйРћгУЙДЙЩЖЈРэМЦЫуГіAPГЄ,НјЖјПЩЕУД№АИЃЎ
![]() ЗжРрЬжТлЃКЕБPЕудкACЩЯ,QдкABЩЯ,дђ
ЗжРрЬжТлЃКЕБPЕудкACЩЯ,QдкABЩЯ,дђ![]() ,
,![]() ,
,![]() ЃЛЕБPЕудкABЩЯ,QдкACЩЯ,дђ
ЃЛЕБPЕудкABЩЯ,QдкACЩЯ,дђ![]() ,
,![]() ,
,![]() ЃЎ
ЃЎ
(1)ЁпЁЯC=90Ёу,![]() ,
,![]() ,
,
![]() ,ЖЏЕуPДгЕуCПЊЪМ,АД
,ЖЏЕуPДгЕуCПЊЪМ,АД![]() ЕФТЗОЖдЫЖЏ,ЫйЖШЮЊУПУы1cm,
ЕФТЗОЖдЫЖЏ,ЫйЖШЮЊУПУы1cm,
![]() ГіЗЂ2УыКѓ,дђ
ГіЗЂ2УыКѓ,дђ![]() ,
,
ЁпЁЯC=90Ёу,
![]() ,
,
![]() ,ЖЏЕуPДгЕуCПЊЪМ,АД
,ЖЏЕуPДгЕуCПЊЪМ,АД![]() ЕФТЗОЖдЫЖЏ,ЧвЫйЖШЮЊУПУы1cm,
ЕФТЗОЖдЫЖЏ,ЧвЫйЖШЮЊУПУы1cm,
![]() дкACЩЯдЫЖЏЪБ
дкACЩЯдЫЖЏЪБ![]() ЮЊжБНЧШ§НЧаЮ,
ЮЊжБНЧШ§НЧаЮ,
![]() ,
,
ШчЭМЃЌЕБPдкABЩЯЪБ,![]() ЪБ,
ЪБ,![]() ЮЊжБНЧШ§НЧаЮ,
ЮЊжБНЧШ§НЧаЮ,
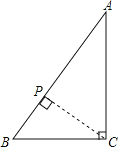
![]() ,
,
![]() ,
,
НтЕУЃК![]() ,
,
![]() ,
,
![]() ,
,
![]() ЫйЖШЮЊУПУы1cm,
ЫйЖШЮЊУПУы1cm,
![]() ,
,
злЩЯЫљЪіЃКЕБ![]() Лђ
Лђ![]() ,
,![]() ЮЊжБНЧШ§НЧаЮЃЛ
ЮЊжБНЧШ§НЧаЮЃЛ
![]() ЕБPЕудкACЩЯ,QдкABЩЯ,дђ
ЕБPЕудкACЩЯ,QдкABЩЯ,дђ![]() ,
,![]() ,
,
![]() жБЯпPQАб
жБЯпPQАб![]() ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗж,
ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗж,
![]() ,
,![]() ЃЛ
ЃЛ
ЕБPЕудкABЩЯ,QдкACЩЯ,дђ![]() ,
,![]() ,
,
![]() жБЯпPQАб
жБЯпPQАб![]() ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗж,
ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗж,
![]() ,
,
![]() ,
,
![]() ЕБ
ЕБ![]() Лђ6УыЪБ,жБЯпPQАб
Лђ6УыЪБ,жБЯпPQАб![]() ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗжЃЎ
ЕФжмГЄЗжГЩЯрЕШЕФСНВПЗжЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
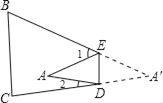
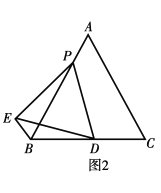
ЁОЬтФПЁПШчЭМЃЌАбЁїABCжНЦЌбиDEелЕўЃЌЕБЕуAТфдкЫФБпаЮBCDEФкВПЪБЃЌ
ЃЈ1ЃЉЩшЁЯAEDЕФЖШЪ§ЮЊxЃЌЁЯADEЕФЖШЪ§ЮЊyЃЌФЧУДЁЯ1ЁЂЁЯ2ЕФЖШЪ§ЗжБ№ЪЧЖрЩйЃПЃЈгУКЌгаxЛђyЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЁЯAгыЁЯ1+ЁЯ2жЎМфгавЛжжЪ§СПЙиЯЕЪМжеБЃГжВЛБфЃЌЧыевГіетИіЙцТЩЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПРЌЛјЕФЗжРрДІРэгыЛиЪеРћгУЃЌПЩвдМѕЩйЮлШОЃЌНкЪЁзЪдДЃЎФГГЧЪаЛЗБЃВПУХЮЊСЫЬсИпаћДЋЪЕаЇЃЌГщбљЕїВщСЫВПЗжОгУёаЁЧјвЛЖЮЪБМфФкЩњЛюРЌЛјЕФЗжРрЧщПіЃЌЦфЯрЙиаХЯЂШчЯТЃК
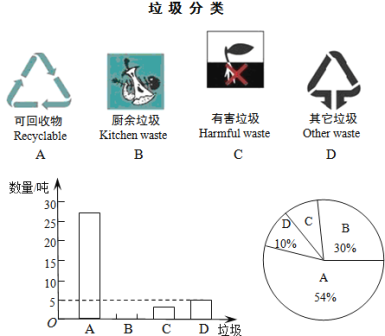
ИљОнЭМБэНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМбљжаЃЌВњЩњЕФгаКІРЌЛјCЫљЖдгІЕФдВаФНЧ ЖШЃЛ
ЃЈ3ЃЉЕїВщЗЂЯжЃЌдкПЩЛиЪеЮяжаЫмСЯРрРЌЛјеМ13%ЃЌУПЛиЪе1ЖжЫмСЯРрРЌЛјПЩЛёЕУ0.5ЖжЖўМЖдСЯЃЎМйЩшИУГЧЪаУПдТВњЩњЕФЩњЛюРЌЛјЮЊ1000ЖжЃЌЧвШЋВПЗжРрДІРэЃЌФЧУДУПдТЛиЪеЕФЫмСЯРрРЌЛјПЩвдЛёЕУЖрЩйЖжЖўМЖдСЯЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЪЧФГаЃЁАКгФЯЪЁККзгЬ§аДДѓШќГѕШќЁБЙкОќзщГЩдБЕФФъСфЗжВМ
ФъСф/Ыъ | 12 | 13 | 14 | 15 |
ШЫЪ§ | 5 | 15 | x | 12Љx |
ЖдгкВЛЭЌЕФxЃЌЯТСаЙигкФъСфЕФЭГМЦСПВЛЛсЗЂЩњИФБфЕФЪЧЃЈЁЁЁЁЃЉ
A. ЦНОљЪ§ЁЂжаЮЛЪ§ B. ЦНОљЪ§ЁЂЗНВю C. жкЪ§ЁЂжаЮЛЪ§ D. жаЮЛЪ§ЁЂЗНВю
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() дк
дк![]() жсЩЯЃЌЕу
жсЩЯЃЌЕу![]() ЁЂ
ЁЂ![]() дк
дк![]() жсЩЯЃЌ
жсЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЪЧ
ЕФзјБъЪЧ![]() ЃЌ
ЃЌ
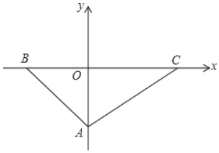
ЃЈ1ЃЉЧѓ![]() Ш§ИіЖЅЕу
Ш§ИіЖЅЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉСЌНг![]() ЁЂ
ЁЂ![]() ЃЌВЂгУКЌзжФИ
ЃЌВЂгУКЌзжФИ![]() ЕФЪНзгБэЪО
ЕФЪНзгБэЪО![]() ЕФУцЛ§ЃЈ
ЕФУцЛ§ЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЮЪЕФЬѕМўЯТЃЌЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЕФУцЛ§ЃПШчЙћДцдкЃЌЧыЧѓГіЕу
ЕФУцЛ§ЃПШчЙћДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкHЃЌЙ§CDбгГЄЯпЩЯвЛЕуEзїЁбOЕФЧаЯпНЛABЕФбгГЄЯпгкFЃЌЧаЕуЮЊGЃЌСЌНгAGНЛCDгкKЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКKE=GEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгCABGЃЌШєЁЯFGB=![]() ЁЯACHЃЌЧѓжЄЃКCAЁЮFEЃЛ
ЁЯACHЃЌЧѓжЄЃКCAЁЮFEЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгCGНЛABгкЕуNЃЌШєsinE=![]() ЃЌAK=
ЃЌAK=![]() ЃЌЧѓCNЕФГЄЃЎ
ЃЌЧѓCNЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌ
жаЃЌ![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
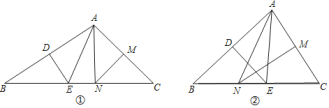
ЃЈ1ЃЉЧыХаЖЯЁїANEЕФжмГЄгыAB+ACЕФКЭЕФДѓаЁ,ВЂЫЕУїРэгЩ.
ЃЈ2ЃЉЂйШчЭМЂйЃЌШєЁЯB=34ЁуЃЌЁЯC=28ЁуЃЌЧѓ![]() ЕФЖШЪ§ЮЊ______ЃЛ
ЕФЖШЪ§ЮЊ______ЃЛ
ЂкШчЭМЂкЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФЖШЪ§ЮЊ________ЃЛ
ЕФЖШЪ§ЮЊ________ЃЛ
ЂлШє![]()
![]() ЃЌдђ
ЃЌдђ![]() ЕФЖШЪ§ЮЊ________.
ЕФЖШЪ§ЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() ЃЌНсТлЃКЂй
ЃЌНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЌЦфжае§ШЗЕФЪЧгаЃЈ ЃЉ
ЃЌЦфжае§ШЗЕФЪЧгаЃЈ ЃЉ
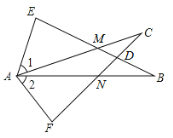
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕШБпШ§НЧаЮ![]() жа
жа![]() Еу
Еу![]() ЪЧ
ЪЧ![]() БпЩЯЕФвЛЕуЃЌЕу
БпЩЯЕФвЛЕуЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯЕФвЛЕуЃЌСЌНг
БпЩЯЕФвЛЕуЃЌСЌНг![]() вд
вд![]() ЮЊБпзїЕШБпШ§НЧаЮ
ЮЊБпзїЕШБпШ§НЧаЮ![]() СЌНг
СЌНг![]() ЃЎ
ЃЎ
![]() ШчЭМ1ЃЌЕБЕу
ШчЭМ1ЃЌЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌ
жиКЯЪБЃЌ
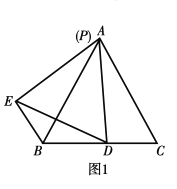
![]() евГіЭМжаЕФвЛЖдШЋЕШШ§НЧаЮЃЌВЂжЄУїЃЛ
евГіЭМжаЕФвЛЖдШЋЕШШ§НЧаЮЃЌВЂжЄУїЃЛ
![]() ЃЛ
ЃЛ
![]() ШчЭМ2ЃЌШє
ШчЭМ2ЃЌШє![]() ЧыМЦЫу
ЧыМЦЫу![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com