
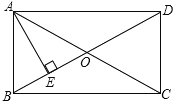
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6. (1)求∠BAE的度数;(2)求AE的长.
【答案】(1)、30°;(2)、3.
【解析】
试题分析:(1)、根据矩形的性质可得:OB=OD,OA=OC,AC=BD,OA=OB,根据BE:ED=1:3,得出BE:OB=1:2,从而说明BE=0E,得出△ABE和△AEO全等,从而得出△AOB为等边三角形,根据等边三角形的性质得出∠BAE的度数;(2)、根据等边三角形的性质得出∠ADE的度数,然后根据直角三角形的性质求出AE的长度.
试题解析:(1)、∵四边形ABCD是矩形,∴OB=OD,OA=OC,AC=BD,∴OA=OB
∵BE:ED=1:3,∴BE:OB=1:2,∴BE=OE ∵AE⊥BD∴![]()
在△AEB和△AEO中 ∴△AEB≌△AEO ∴AB=AO,∴OA=AB=OB,
∴△AEB≌△AEO ∴AB=AO,∴OA=AB=OB,
即△OAB是等边三角形,∴∠BAE=30°
(2)、∵△OAB是等边三角形,∴∠ABD=60° ∴∠ADE=90°﹣∠ABD=30°
∵AE⊥BD,AD=6,∴AE=![]() AD=3.
AD=3.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】今年,6月12日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.

(1)小华的问题解答:
(2)小明的问题解答:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
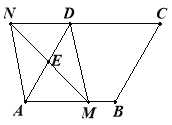
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分) 若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“兄弟二次函数”.
(1)请写出两个为“兄弟二次函数”的函数;
(2)已知关于x的二次函数y1=2x2﹣4mx+2m2+1和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2与y1为“兄弟二次函数”,求函数y2的表达式,并直接写出当0≤x≤3时,y2的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com