

分析 (1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;
(2)设出点P的坐标,①用△POA的面积是△POB面积的$\frac{4}{3}$倍,建立方程求解即可;②利用对称性找到最小线段,用两点间距离公式求解即可;
(3)分OB为边和为对角线两种情况进行求解,①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;
②当OB为对角线时,OB与MN互相平分,交点为H,设出M,N坐标用OH=BH,MH=NH,建立方程组求解即可.
解答 解:(1)∵直线y=-$\frac{1}{2}$x+1与x轴交于点A,与y轴交于点B,
∴A(2,0),B(0,1),
∵抛物线y=-x2+bx+c经过A、B两点,
∴$\left\{\begin{array}{l}{-4+2b+c=0}\\{c=1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{c=1}\end{array}\right.$
∴抛物线解析式为y=-x2+$\frac{3}{2}$x+1,
(2)①由(1)知,A(2,0),B(0,1),
∴OA=2,OB=1,
由(1)知,抛物线解析式为y=-x2+$\frac{3}{2}$x+1,
∵点P是第一象限抛物线上的一点,
∴设P(a,-a2+$\frac{3}{2}$a+1),((a>0,-a2+$\frac{3}{2}$a+1>0),
∴S△POA=$\frac{1}{2}$OA×Py=$\frac{1}{2}$×2×(-a2+$\frac{3}{2}$a+1)=-a2+$\frac{3}{2}$a+1
S△POB=$\frac{1}{2}$OB×Px=$\frac{1}{2}$×1×a=$\frac{1}{2}$a
∵△POA的面积是△POB面积的$\frac{4}{3}$倍.
∴-a2+$\frac{3}{2}$a+1=$\frac{4}{3}$×$\frac{1}{2}$a,
∴a=$\frac{3}{2}$或a=-$\frac{2}{3}$(舍)
∴P($\frac{3}{2}$,1);
②如图1,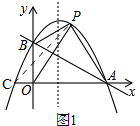
由(1)知,抛物线解析式为y=-x2+$\frac{3}{2}$x+1,
∴抛物线的对称轴为x=$\frac{3}{4}$,抛物线与x轴的另一交点为C(-$\frac{1}{2}$,0),
∵点A与点C关于对称轴对称,
∴QP+QA的最小值就是PC=$\sqrt{5}$;
(3)①当OB为平行四边形的边时,MN=OB=1,MN∥OB,
∵点N在直线AB上,
∴设M(m,-$\frac{1}{2}$m+1),
∴N(m,-m2+$\frac{3}{2}$m+1),
∴MN=|-m2+$\frac{3}{2}$m+1-(-$\frac{1}{2}$m+1)|=|m2-2m|=1,
Ⅰ、m2-2m=1,
解得,m=1±$\sqrt{2}$,
∴M(1+$\sqrt{2}$,$\frac{1}{2}$(1-$\sqrt{2}$))或M(1-$\sqrt{2}$,$\frac{1}{2}$(1+$\sqrt{2}$))
Ⅱ、m2-2m=-1,
解得,m=1,
∴M(1,$\frac{1}{2}$);
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,1),O(0,0),
∴H(0,$\frac{1}{2}$),
设M(n,-$\frac{1}{2}$n+1),N(d,-d2+$\frac{3}{2}$d+1)
∴$\left\{\begin{array}{l}{\frac{n+d}{2}=0}\\{\frac{-\frac{1}{2}n+1-{d}^{2}+\frac{3}{2}d+1}{2}=\frac{1}{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{d=1+\sqrt{2}}\\{n=-(1+\sqrt{2})}\end{array}\right.$或$\left\{\begin{array}{l}{d=1-\sqrt{2}}\\{n=-(1-\sqrt{2})}\end{array}\right.$,
∴M(-(1+$\sqrt{2}$),$\frac{1}{2}$(3+$\sqrt{2}$))或M(-(1-$\sqrt{2}$),$\frac{1}{2}$(3-$\sqrt{2}$));
即:满足条件的点M的坐标(1+$\sqrt{2}$,$\frac{1}{2}$(1-$\sqrt{2}$))或(1-$\sqrt{2}$,-$\frac{1}{2}$(1+$\sqrt{2}$))或(1,$\frac{1}{2}$)或M(-(1+$\sqrt{2}$),$\frac{1}{2}$(3+$\sqrt{2}$))或M(-(1-$\sqrt{2}$),$\frac{1}{2}$(3-$\sqrt{2}$));
点评 此题是二次函数综合题,主要考查了待定系数法,三角形的面积,平行四边形的性质,对称性,解本题的关键是求抛物线解析式,确定最小值和点M坐标时,分类讨论是解本题的难点.


科目:初中数学 来源: 题型:填空题
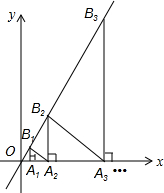 如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是(2×3n-1,0).
如图,在坐标轴上取点A1(2,0),作x轴的垂线与直线y=2x交于点B1,作等腰直角三角形A1B1A2;又过点A2作x轴的垂线交直线y=2x交于点B2,作等腰直角三角形A2B2A3;…,如此反复作等腰直角三角形,当作到An(n为正整数)点时,则An的坐标是(2×3n-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)3=-8 | B. | (-1)2016=1 | C. | (-$\frac{1}{2}$)4×(-1)3=$\frac{1}{16}$ | D. | (-3)3×(-1)4=-27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com