
【题目】如图所示,在![]() ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°.请探索BM,DN与AB的数量关系,并证明你的结论.
ABCD中,∠ABC=60°,且AB=BC,∠MAN=60°.请探索BM,DN与AB的数量关系,并证明你的结论.
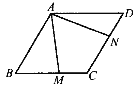
【答案】BM+DN=AB
【解析】
试题分析:连结AC,先由证∠ABC=60°,AB=BC,证得△ABC为等边三角形,再结合平行四边形的性质即可得到△ABM≌△CAN,从而得到BM=CN,即可得到结果。
如图,连结AC,
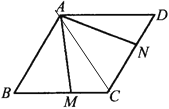
∵![]() ABCD,∠ABC=60°,
ABCD,∠ABC=60°,
∴AB=CD,∠BAD=120°,AB∥CD,
∵∠MAN=60°,
∴∠MAC+∠NAC =60°,
∵∠ABC=60°,AB=BC,
∴△ABC为等边三角形,
∴∠BAC=∠BCA=60°,AB=BC=AC,
∴∠BAM+∠NAC =60°,
∴∠BAM=∠NAC,
∵AB∥CD,
∴∠BAC=∠DCA=60°,
∵∠BAM=∠NAC,AB=AC,∠ABC=∠DCA=60°,
∴△ABM≌△CAN,
∴BM=CN,
∵AB=CD,
∴BM+DN= CN+DN=CD=AB.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C 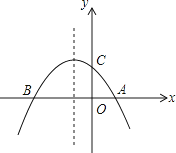
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若∠1=100°,∠4=80°,则__________,理由是________________;若∠3=70°,则∠2=_______时,也可推出AB∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).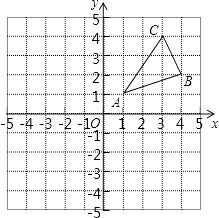
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于原点对称的△A2B2C2;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖州市在2017年被评为“全国文明城市”,在评选过程中,湖州市环卫处每天需负责市区范围420千米城市道路的清扫工作,现有环卫工人直接清扫和道路清扫车两种马路清扫方式.已知20名环卫工人和1辆道路清扫车每小时可以清扫20千米马路,30名环卫工人和3辆道路清扫车每小时可以清扫42千米的马路.
(1)1名环卫工人和1辆道路清扫车每小时各能清扫多长的马路?
(2)已知2017年环卫处安排了50名环卫工人参与了直接清扫工作,为保证顺利完成每日的420千米清扫工作,需派出多少辆道路清扫车参与工作(已知2017年环卫工人与清扫车每天工作时间为6小时)?
(3)为了巩固文明城市创建成果,从2018年5月开始,环卫处新增了一辆清扫车参与工作,同时又增加了若干个环卫工人参与直接清扫,使得每日能够较早的完成清扫工作。2018年6月市环卫处扩大清扫范围60千米,同时又增加了20名环卫工人直接参与清扫,此时环卫工人和清扫车每日工作时间仍与5月份相同,那么2018年5月环卫处增加了多少名环卫工人参与直接清扫?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出): 
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有5张写着不同数的卡片,请你分别按要求抽出卡片,写出符合要求的算式:
![]()
(1)从中取出2张卡片,使这2张卡片上的数的乘积最大;
(2)从中取出2张卡片,使这2张卡片上的数相除的商最小;
(3)从中取出2张卡片,使这2张卡片上的数通过有理数的运算后得到的结果最大;
(4)从中取出4张卡片,使这4张卡片通过有理数的运算后得到的结果为24.(写出一种即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com