
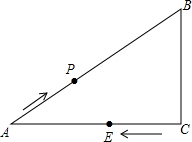
 如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢?
如图:在△ABC,∠C=90°,AB=10,AC=8,P为AB上一动点,以每秒2个单位的速度从A向B点运动,点E以每秒1个单位速度从点C出发向A点运动,问经几秒后以A,P,E为顶点的三角形和△ABC相似?如果点E改为C出发向点B运动,情况又怎样了呢? 分析 需要分类讨论:∠AEP=90°或∠APE=90°两种情况.结合相似三角形的对应边成比例进行解答.
解答 解:设经过t秒,后以A,P,E为顶点的三角形和△ABC相似.
①当△AEP∽△ABC时,$\frac{AE}{AB}$=$\frac{AP}{AC}$,即$\frac{8-t}{10}$=$\frac{2t}{8}$,
解得t=$\frac{16}{7}$;
②当△APE∽△ABC时,$\frac{AE}{AC}$=$\frac{AP}{AB}$,即$\frac{8-t}{8}$=$\frac{2t}{10}$,
解得t=$\frac{40}{13}$;
综上所述,经$\frac{16}{7}$或$\frac{40}{13}$秒后以A,P,E为顶点的三角形和△ABC相似.
如果点E改为C出发向点B运动,由于△APE不是直角三角形,所以这两个三角形不可能相似.
点评 本题考查了相似三角形的判定.对于动点问题,应该分类讨论,以防漏解.


科目:初中数学 来源: 题型:填空题
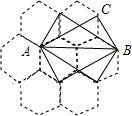 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的蜂型网络,正六边形的顶点称为格点,如果一个三角形的三个顶点都在格点上,称之为格点三角形.如图以AB为斜边的格点直角三角形共有4个,△ABC是其中之一,则在蜂巢型网络中,与△ABC全等的格点三角形(包括△ABC)共有84.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
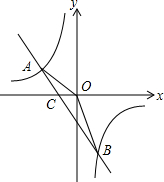 已知反比例函数y=$\frac{{k}_{1}}{3x}$的图象与一次函数y=k2x+m的图象交于A(-1,a),B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{{k}_{1}}{3x}$的图象与一次函数y=k2x+m的图象交于A(-1,a),B($\frac{1}{3}$,-3)两点,连结AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
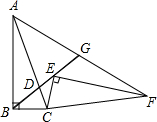 如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.
如图,在Rt△ABC中,∠ABC=90°,sin∠BAC=$\frac{1}{3}$,点D是AC上一点,且BC=BD=2,将Rt△ABC绕点C旋转到Rt△FEC的位置,并使点E在射线BD上,连接AF交射线BD于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com