
【题目】将若干个奇数按每行8个数排成如图的形式:

小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
【答案】(1)189;(2)19;(3)方框内的9个数之和总是9的倍数
【解析】
(1)根据已知9个数直接求出和即可,进而得出与中间的数的关系;
(2)根据(1)中规律得出方框,左下角的那个数即可;
(3)设中间的数为x,分别表示出其它8个数,进一步求和得出答案即可.
(1)3+5+7+19+21+23+35+37+39=21×9=189;
(2)这个方框内左下角的数为333÷9-2-16=19;
(3)设中间一个数为x,则9个数之和为:
(x-18)+(x-16)+(x-14)+(x-2)+x+(x+2)+(x+14)+(x+16)+(x+18)=9x.
方框内9个数之和为9x,
∴方框内的9个数之和总是9的倍数


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某校在开发区一块宽为120m的矩形用地上新建分校区,规划图纸上把它分成①②③三个区域,区域①和区域②为正方形,区域①为教学区;区域②为生活区;区域③为活动区,设这块用地长为xm,区域③的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)若区域③的面积为3200m2,那么这块用地的长应为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
(1)操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .
(2)猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.
(3)延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PAPB=kAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
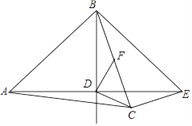
【题目】如图,在△ABC中,AB=AC,点D是△ABC内一点,AD=BD,且AD⊥BD,连接CD.过点C作CE⊥BC交AD的延长线于点 E,连接BE.过点D作DF⊥CD交BC于点F.
(1)若BD=DE=![]() ,CE=
,CE=![]() ,求BC的长;
,求BC的长;
(2)若BD=DE,求证:BF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④ . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()

显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() ,线段
,线段![]() .
.
(1)如图,若点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,则线段
的中点,则线段![]() 的长度是 ;
的长度是 ;
![]()
(2)若把(1)中点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,改为点
,改为点![]() 是线段
是线段![]() 上任意一点,且
上任意一点,且![]() ,
,![]() ,其他条件不变,请求出线段
,其他条件不变,请求出线段![]() 的长度(用含
的长度(用含![]() 、
、![]() 的式子表示);
的式子表示);
(3)若把(2)中点![]() 是线段
是线段![]() 上任意一点,改为点
上任意一点,改为点![]() 是直线
是直线![]() 上任意一点,其他条件不变,则线段
上任意一点,其他条件不变,则线段![]() 的长度会变化吗?若有变化,求出结果.
的长度会变化吗?若有变化,求出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若OC是∠AOB内部的一条射线,则下列式子中,不能表示“OC是∠AOB的平分线”的是( )
A. ∠AOC=∠BOC B. ∠AOB=2∠BOC
C. ∠AOC=![]() ∠AOB D. ∠AOC+∠BOC=∠AOB
∠AOB D. ∠AOC+∠BOC=∠AOB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD 中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N ,连接OM,ON,MN .下列五个结论:①△CNB≌△DMC ;②△CON≌△DOM ;③△OMN≌△OAD ;④![]() ;⑤若AB=2,则
;⑤若AB=2,则![]() 的最小值是
的最小值是![]() ,其中正确结论的个数是 ( )
,其中正确结论的个数是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)将两条宽度一样的矩形纸条如图交叉,请判断重叠部分是一个什么图形?并证明你的结论。
(2) 若两张矩形纸条的长度均为8,宽度均为2,请求出重叠部分的图形的周长的最大值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com