
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
| A. | 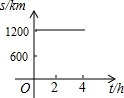 | B. | 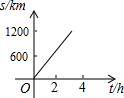 | C. | 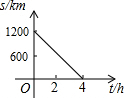 | D. | 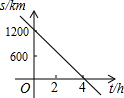 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
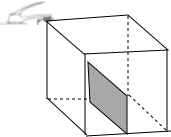 如图,在一个正方体容器底部正中央嵌入一块平行于侧面的矩形隔板,隔板的高是正方体棱长的一半,现匀速向隔板左侧注水(到容器注满时停止),设注水时间为t(min),隔板所在平面左侧的水深为y左(cm),则y左与t的函数图象大致是( )
如图,在一个正方体容器底部正中央嵌入一块平行于侧面的矩形隔板,隔板的高是正方体棱长的一半,现匀速向隔板左侧注水(到容器注满时停止),设注水时间为t(min),隔板所在平面左侧的水深为y左(cm),则y左与t的函数图象大致是( )| A. |  | B. | 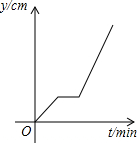 | C. | 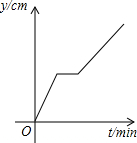 | D. | 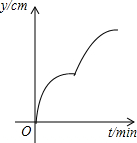 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
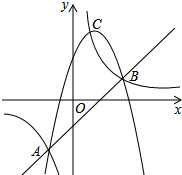 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论:
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3中最小的函数值},则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com