
”¾ĢāÄæ”æijľ°å¼Ó¹¤³§½«¹ŗ½ųµÄAŠĶ”¢BŠĶĮ½ÖÖľ°å¼Ó¹¤³ÉCŠĶ£¬DŠĶĮ½ÖÖľ°å³öŹŪ£¬ŅŃÖŖŅ»æéAŠĶľ°åµÄ½ų¼Ū±ČŅ»æéBŠĶľ°åµÄ½ų¼ŪÉŁ10ŌŖ£¬ĒŅ¹ŗĀņ3æéAŠĶľ°åŗĶ2æéBŠĶľ°å¹²»Ø·Ń120ŌŖ£®
£Ø1£©AŠĶľ°åÓėBŠĶľ°åµÄ½ų¼Ūø÷ŹĒ¶ąÉŁŌŖ£æ
£Ø2£©øł¾ŻŹŠ³”ŠčĒó£¬øĆľ°å¼Ó¹¤³§¾ö¶ØÓĆ²»³¬¹ż2770ŌŖ¹ŗ½ųAŠĶľ°å”¢BŠĶľ°å¹²100æ飬ČōŅ»æéAŠĶľ°åæÉÖĘ³É1æéCŠĶľ°å”¢2æéDŠĶľ°å£»Ņ»æéBŠĶľ°åæÉÖĘ³É2æéCŠĶľ°å”¢1æéDŠĶľ°å£¬ĒŅÉś²ś³öĄ“µÄCŠĶľ°åŹżĮæ²»ÉŁÓŚDŠĶľ°åµÄŹżĮæµÄ7/5£®
¢ŁøĆľ°å¼Ó¹¤³§ÓŠ¼øÖÖ½ų»õ·½°ø£æ
¢ŚČōCŠĶľ°åĆææéŹŪ¼Ū30ŌŖ£¬DŠĶľ°åĆææéŹŪ¼Ū25ŌŖ£¬ĒŅÉś²ś³öĄ“µÄCŠĶľ°å”¢DŠĶľ°åČ«²æŹŪ³ö£¬ÄÄŅ»ÖÖ·½°ø»ńµĆµÄĄūČó×ī“ó£¬Ēó³ö×ī“óĄūČóŹĒ¶ąÉŁ£æ
”¾“š°ø”æ£Ø1£©AŠĶľ°åµÄ½ų¼ŪĪŖ20ŌŖ£¬BŠĶľ°åµÄ½ų¼ŪĪŖ30ŌŖ£»£Ø2£©¢ŁøĆľ°å¼Ó¹¤³§¹²ÓŠ3ÖÖ½ų»õ·½°ø£¬·½°ø1£ŗ¹ŗ½ų23æéAŠĶľ°å£¬77æéBŠĶľ°å£»·½°ø2£ŗ¹ŗ½ų24æéAŠĶľ°å76æéBŠĶľ°å£»·½°ø3£ŗ¹ŗ½ų25æéAŠĶľ°å£¬75æéBŠĶľ°å£®¢Ś·½°ø3¹ŗ½ų25æéAŠĶľ°å£¬75æéBŠĶľ°å»ńµĆµÄĄūČó×ī“ó£¬×ī“óĄūČóĪŖ5625ŌŖ£®
”¾½āĪö”æ
£Ø1£©ÉčAŠĶľ°åµÄ½ų¼ŪĪŖxŌŖ£¬BŠĶľ°åµÄ½ų¼ŪĪŖyŌŖ£¬øł¾Ż”°Ņ»æéAŠĶľ°åµÄ½ų¼Ū±ČŅ»æéBŠĶľ°åµÄ½ų¼ŪÉŁ10ŌŖ£¬¹ŗĀņ3æéAŠĶľ°åŗĶ2æéBŠĶľ°å¹²»Ø·Ń120ŌŖ”±£¬¼“æÉµĆ³ö¹ŲÓŚx£¬yµÄ¶žŌŖŅ»“Ī·½³Ģ×飬½āÖ®¼“æÉµĆ³ö½įĀŪ£»
£Ø2£©¢ŁÉč¹ŗ½ųmæéAŠĶľ°å£¬Ōņ¹ŗ½ų£Ø100©m£©æéBŠĶľ°å£¬øł¾Ż¹ŗ½ų100æéľ°åµÄ×Ü·ŃÓĆ²»³¬¹ż2770ŌŖĒŅÉś²ś³öĄ“µÄCŠĶľ°åŹżĮæ²»ÉŁÓŚDŠĶľ°åµÄŹżĮæµÄ![]() £¬¼“æÉµĆ³ö¹ŲÓŚmµÄŅ»ŌŖŅ»“Ī²»µČŹ½×飬½āÖ®¼“æÉµĆ³ömµÄȔֵ·¶Ī§£¬½įŗĻmĪŖÕūŹż¼“æÉµĆ³öø÷½ų»õ·½°ø£»
£¬¼“æÉµĆ³ö¹ŲÓŚmµÄŅ»ŌŖŅ»“Ī²»µČŹ½×飬½āÖ®¼“æÉµĆ³ömµÄȔֵ·¶Ī§£¬½įŗĻmĪŖÕūŹż¼“æÉµĆ³öø÷½ų»õ·½°ø£»
¢Śøł¾ŻĄūČó£½ĻśŹŪŹÕČė©³É±¾£¬¼“æÉ·Ö±šĒó³öČżøö·½°ø»ńµĆµÄĄūČó£¬±Č½Ļŗó¼“æÉµĆ³ö½įĀŪ£®
£Ø1£©ÉčAŠĶľ°åµÄ½ų¼ŪĪŖxŌŖ£¬BŠĶľ°åµÄ½ų¼ŪĪŖyŌŖ£¬
ŅĄĢāŅā£¬µĆ£ŗ![]() £¬
£¬
½āµĆ£ŗ![]() £®
£®
“š£ŗAŠĶľ°åµÄ½ų¼ŪĪŖ20ŌŖ£¬BŠĶľ°åµÄ½ų¼ŪĪŖ30ŌŖ£®
£Ø2£©¢ŁÉč¹ŗ½ųmæéAŠĶľ°å£¬Ōņ¹ŗ½ų£Ø100©m£©æéBŠĶľ°å£¬
ŅĄĢāŅā£¬µĆ£ŗ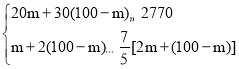 £¬
£¬
½āµĆ£ŗ23”Üm”Ü25£®
”ßmĪŖÕūŹż£¬
”ąm£½23£¬24£¬25£¬
”ąøĆľ°å¼Ó¹¤³§¹²ÓŠ3ÖÖ½ų»õ·½°ø£¬·½°ø1£ŗ¹ŗ½ų23æéAŠĶľ°å£¬77æéBŠĶľ°å£»·½°ø2£ŗ¹ŗ½ų24æéAŠĶľ°å£¬76æéBŠĶľ°å£»·½°ø3£ŗ¹ŗ½ų25æéAŠĶľ°å£¬75æéBŠĶľ°å£»
¢Ś·½°ø1»ńµĆµÄĄūČóĪŖ30”Į£Ø23+2”Į77£©+25”Į£Ø2”Į23+77£©©20”Į23©30”Į77£½5615£ØŌŖ£©£¬
·½°ø2»ńµĆµÄĄūČóĪŖ30”Į£Ø24+2”Į76£©+25”Į£Ø2”Į24+76£©©20”Į24©30”Į76£½5620£ØŌŖ£©£¬
·½°ø3»ńµĆµÄĄūČóĪŖ30”Į£Ø25+2”Į75£©+25”Į£Ø2”Į25+75£©©20”Į25©30”Į75£½5625£ØŌŖ£©£¬
”ß5615£¼5620£¼5625£¬
”ą·½°ø3¹ŗ½ų25æéAŠĶľ°å£¬75æéBŠĶľ°å»ńµĆµÄĄūČó×ī“ó£¬×ī“óĄūČóĪŖ5625ŌŖ£®


 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓĆŅ»Ńł³¤µÄŠ”ľ°ō°“ĻĀĶ¼ÖŠµÄ·½Ź½“īĶ¼ŠĪ.
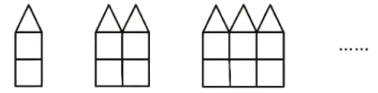
£Ø1£©°“Ķ¼Ź¾¹ęĀÉĢīæÕ£ŗ
Ķ¼ŠĪ±źŗÅ | ¢Ł | ¢Ś | ¢Ū | ” |
Š”ľ°ōµÄøłŹż | 9 | ” |
£Ø2£©°“ÕÕÕāÖÖ¹ęĀÉ“īĻĀČ„£¬“īµŚ![]() øöĶ¼ŠĪŠčŅŖ________øłŠ”ľ°ō£»
øöĶ¼ŠĪŠčŅŖ________øłŠ”ľ°ō£»
£Ø3£©ĒėĒó³ö“īµŚ100øöĶ¼ŠĪŠčŅŖµÄŠ”ľ°ōµÄøłŹż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćA”¢D”¢C”¢FŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬AB=DE£¬BC=EF£¬ŅŖŹ¹”÷ABC”Õ”÷DEF£¬»¹ŠčŅŖĢķ¼ÓŅ»øöĢõ¼žŹĒ£Ø””””£©

A. ”ĻBCA=”ĻF£» B. ”ĻB=”ĻE£» C. BC”ĪEF £» D. ”ĻA=”ĻEDF
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠ![]() 暰ײĖ,ŅŌĆææš
暰ײĖ,ŅŌĆææš![]() Ē§æĖĪŖ±ź×¼,³¬¹ż»ņ²»×ćµÄ·Ö±šÓĆÕż”¢øŗĄ“±ķŹ¾,¼ĒĀ¼ČēĻĀ£ŗ
Ē§æĖĪŖ±ź×¼,³¬¹ż»ņ²»×ćµÄ·Ö±šÓĆÕż”¢øŗĄ“±ķŹ¾,¼ĒĀ¼ČēĻĀ£ŗ
Óė±ź×¼ÖŹĮæµÄ²ī |
|
|
|
|
|
|
æš Źż |
|
|
|
|
|
|
(1)Óė±ź×¼ÖŹĮæ±Č½Ļ,![]() 暰ײĖ×Ü¼Ę³¬¹ż»ņ²»×涹ɣĒ§æĖ£æ
暰ײĖ×Ü¼Ę³¬¹ż»ņ²»×涹ɣĒ§æĖ£æ
(2)Čō°×²ĖĆæĒ§æĖŹŪ¼Ū![]() ŌŖ,Ōņ³öŹŪÕā
ŌŖ,Ōņ³öŹŪÕā![]() 暰ײĖæÉĀō¶ąÉŁŌŖ£æ
暰ײĖæÉĀō¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖ½āøßŅ»Äź¼¶×”Š£ÉśŌŚŠ£ĘŚ¼äµÄŌĀÉś»īÖ§³öĒéæö£¬“ÓøßŅ»Äź¼¶600Ćū×”Š£Ń§ÉśÖŠĖ껜³éČ”²æ·Öѧɜ£¬¶ŌĖūĆĒ½ńÄź4ŌĀ·ŻµÄÉś»īÖ§³öĒéæö½ųŠŠµ÷²éĶ³¼Ę£¬²¢»ęÖĘ³ÉČēĻĀĶ³¼ĘĶ¼±ķ£ŗ

Ēėøł¾ŻĶ¼±ķÖŠĖłøųµÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ŌŚÕā“Īµ÷²éÖŠ¹²Ė껜³éČ”ĮĖ Ćūѧɜ£¬Ķ¼±ķÖŠµÄm= £¬n= £»
£Ø2£©Ēė¹Ą¼ĘøĆŠ£øßŅ»Äź¼¶600Ćū×”Š£Ń§Éś½ńÄź4ŌĀ·ŻÉś»īÖ§³öµĶÓŚ350ŌŖµÄѧɜČĖŹż£»
£Ø3£©ĻÖÓŠŅ»Š©°®ŠÄČĖŹæÓŠŅāŌø׏֜øĆŠ£¼ŅĶ„Ą§ÄѵÄѧɜ£¬Ń§Š£ŌŚ±¾“Īµ÷²éµÄ»ł“”ÉĻ£¬¾¹ż½ųŅ»²½ŗĖŹµ£¬Č·ČĻøßŅ»£Ø2£©°ąÓŠA£¬B£¬CČżĆūѧɜ¼ŅĶ„Ą§ÄŃ£¬ĘäÖŠA£¬BĪŖÅ®Éś£¬CĪŖÄŠÉś. Ąī°¢ŅĢÉźĒė׏֜ĖūĆĒÖŠµÄĮ½Ćū£¬ÓŚŹĒѧŠ£ČĆĄī°¢ŅĢ“ÓA£¬B£¬CČżĆūѧɜ֊ŅĄ“ĪĖ껜³éČ”Į½Ćūѧɜ½ųŠŠ×ŹÖś£¬ĒėÓĆĮŠ±ķ·Ø£Ø»ņŹ÷דĶ¼·Ø£©ĒóĒ”ŗĆ³éµ½A£¬BĮ½ĆūÅ®ÉśµÄøÅĀŹ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAŌŚµŚŅ»ĻóĻŽ£¬AB”ĶxÖįÓŚB£®AC”ĶyÖįÓŚC£¬A£Ø4a£¬3a£©£¬ĒŅĖıߊĪABOCµÄĆ껿ĪŖ48£®
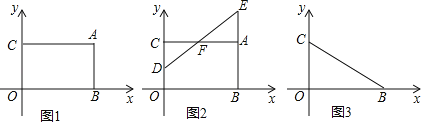
£Ø1£©ČēĶ¼1£¬Ö±½ÓŠ“³öµćAµÄ×ų±ź£»
£Ø2£©ČēĶ¼2£¬µćD“ÓO³ö·¢ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲyÖįÕż°ėÖįŌĖ¶Æ£¬Ķ¬Ź±µćE“ÓA³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲÉäĻßBAŌĖ¶Æ£¬DE½»Ļ߶ĪACÓŚF£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖt£¬µ±S”÷AEF£¼S”÷CDFŹ±£¬ĒótµÄȔֵ·¶Ī§£»
£Ø3£©ČēĶ¼3£¬½«Ļ߶ĪBCĘ½ŅĘ£¬Ź¹µćBµÄ¶ŌÓ¦µćMĒ”ŗĆĀäŌŚyÖįøŗ°ėÖįÉĻ£¬µćCµÄ¶ŌÓ¦µćĪŖN£¬Į¬BN½»yÖįÖįÓŚP£¬µ±OM£½3OPŹ±£¬ĒóµćMµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ,ČēĶ¼,”÷ABCŹĒµČ±ßČż½ĒŠĪ,AE=CD,BQ”ĶADÓŚQ,BE½»ADÓŚµćP,ĻĀĮŠĖµ·Ø£ŗ¢Ł”ĻAPE=”ĻC,¢ŚAQ=BQ,¢ŪBP=2PQ,¢ÜAE+BD=AB,ĘäÖŠÕżČ·µÄøöŹżÓŠ( )øö”£
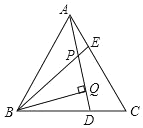
A. 4B. 3C. 2D. 1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
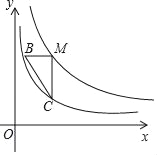
”¾ĢāÄæ”æČēĶ¼£¬µćMŌŚŗÆŹży=![]() £Øx£¾0£©µÄĶ¼ĻóÉĻ£¬¹żµćM·Ö±š×÷xÖįŗĶyÖįµÄĘ½ŠŠĻß½»ŗÆŹży=
£Øx£¾0£©µÄĶ¼ĻóÉĻ£¬¹żµćM·Ö±š×÷xÖįŗĶyÖįµÄĘ½ŠŠĻß½»ŗÆŹży=![]() £Øx£¾0£©µÄĶ¼ĻóÓŚµćB”¢C£®
£Øx£¾0£©µÄĶ¼ĻóÓŚµćB”¢C£®
£Ø1£©ČōµćMµÄ×ų±źĪŖ£Ø1£¬3£©£®
¢ŁĒóB”¢CĮ½µćµÄ×ų±ź£»
¢ŚĒóÖ±ĻßBCµÄ½āĪöŹ½£»
£Ø2£©Ēó”÷BMCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄÕż·½ŠĪĶųøńÖŠ½ØĮ¢ČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµ£¬”÷ABCµÄ¶„µć¶¼ŌŚøńµćÉĻ£¬Ēė½ā“šĻĀĮŠĪŹĢā£ŗ
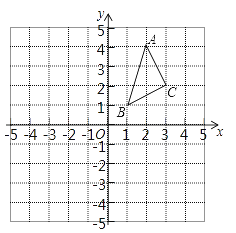
£Ø1£©¢Ł×÷³ö”÷ABCĻņ×óĘ½ŅĘ4øöµ„Ī»³¤¶ČŗóµĆµ½µÄ”÷A1B1C1£¬ ²¢Š“³öµćC1µÄ×ų±ź£»
¢Ś×÷³ö”÷ABC¹ŲÓŚŌµćO¶Ō³ĘµÄ”÷A2B2C2£¬ ²¢Š“³öµćC2µÄ×ų±ź£»
£Ø2£©ŅŃÖŖ”÷ABC¹ŲÓŚÖ±Ļßl¶Ō³ĘµÄ”÷A3B3C3µÄ¶„µćA3µÄ×ų±źĪŖ£Ø£4£¬£2£©£¬ĒėÖ±½ÓŠ“³öÖ±ĻßlµÄŗÆŹż½āĪöŹ½.
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com