练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．我们知道，通过添加平行线，可以得到相等的角．
    （1）如图1，已知△ABC中，∠B=∠C，AD⊥BC于D，若过A点作MN∥BC，请根据图中的辅助线，说明：∠DAB=∠DAC；
    （2）如图2，请用添加平行线的方法解决问题：已知D为∠BAC内一点，连结BD、CD．求证：∠BDC=∠A+∠B+∠C；
    （3）如图3，已知∠A=50°，∠B+∠F=70°，∠F+∠C=60°，∠B+∠C=50°，则∠D+∠E=140°（不写求解过程，直接写出结果）

    分析 （1）先证明DA⊥MN，由∠BAD=90°-∠MAB，∠DAC=90°-∠NAC即可解决问题．
    （2）如图2中，作CM∥AB交BD的延长线于M，根据三角形外角等于不相邻的两个内角和即可解决问题．
    （3）利用（2）的结论即可解决问题．

    解答 解：（1）如图1中，

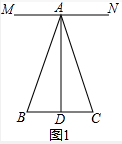
    ∵MN∥BC，
    ∴∠MAB=∠B，∠NAC=∠C，
    ∵∠B=∠C，
    ∴∠MAB=∠NAC，
    ∵AD⊥BC，MN∥BC，
    ∴DA⊥MN，
    ∴∠MAD=∠NAD=90°，
    ∵∠BAD=90°-∠MAB，∠DAC=90°-∠NAC，
    ∴∠BAD=∠CAD．

    （2）如图2中，作CM∥AB交BD的延长线于M．

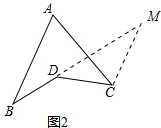
    ∵AB∥CM，
    ∴∠B=∠M，∠A=∠ACM，
    ∴∠BDC=∠DCM+∠M=∠ACD+∠ACM+∠M=∠ACD+∠B+∠A．

    （3）如图3中，连接AF．

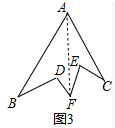
    由（2）可知，∠BDF=∠B+∠BAF+∠AFD，∠FEC=∠C+∠CAF+∠AFE，
    ∴∠D+∠E=∠B+∠BAF+∠AFD+∠AFE+∠FAC+∠C=∠B+∠BAC+∠C+∠DFE．
    ∵∠B+∠F=70°，∠F+∠C=60°，
    ∴∠B+2∠F+∠C=130°，
    ∵∠B+∠C=50°，
    ∴∠F=40°，
    ∴∠D+∠E=50°+50°+40°=140°．
    故答案为140．

    点评 本题考查三角形综合题、等腰三角形的性质、平行线的性质，解题的关键是学会添加辅助线，学会利用结论解决新的问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．如表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2：
    甲乙丙丁
    平均数x（cm）175173175174
    方差S2（cm2）3.53.512.515
    根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择甲．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．因式分解
    （1）-2x2+4x-2
    （2）（x2+4）2-16x2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，已知∠AOB=120°，OA⊥OC，BO⊥OD，则∠COD=60度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在△ABC中，已知AB=AC，∠A=40°，DE垂直平分AC交AB于E，求∠BCE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在直角坐标系中，点A（0，6）、B（8，0），动点P从点A出发在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B出发在线段上以每秒2个单位长度的速度向点A移动，其中一点到达终点时另一点也随之停止，设点P、Q移动的时间为t秒．
    （1）求直线AB的函数解析式；
    （2）在移动的过程中，探究以A，P，Q为顶点的三角形能否与△AOB相似，若能求出t的值，若不能说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．点D在等边三角形△ABC的边BC上，将△ABD绕点A旋转，使得旋转后点B的对应点为点C．
    （1）在图1中画出旋转后的图形．
    （2）小颖是这样做的：如图2，过点C画BA的平行线L，在L上取CE=BD，连接AE，则△ACE即为旋转后的图形．小颖这样做对吗？请你说说理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．己知点A（a，b）是反比例函数y=$\frac{8}{x}$（x＞0）图象上的动点，AB∥x轴，AC∥y轴，分别交反比例函数y=$\frac{k}{x}$（x＞0）的图象于点B、C，交坐标轴于D、E，且AC=3CD，连接BC．
    （1）求k的值；
    （2）在点A运动过程中，设△ABC的面积为S，则S是否变化？若不变，请求出S的值；若改变，请写出S关于a的函数关系式；
    （3）探究：△ABC与以点O、D、E为顶点的三角形是否相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．若$\sqrt{x-12}$+|3-y|=0，则$\sqrt{x}$-$\sqrt{y}$的值为（　　）
    A．9B．-$\sqrt{3}$C．$\sqrt{3}$D．-9

    查看答案和解析>>

    同步练习册答案