
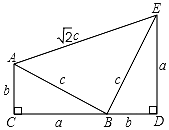
 如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.
如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=$\sqrt{2}$c,这时我们把关于x的形如ax2+$\sqrt{2}$cx+b=0的一元二次方程称为“勾系一元二次方程”.分析 (1)只要证明△≥0即可解决问题.
(2)当x=-1时,有a-$\sqrt{2}$c+b=0,即a+b=$\sqrt{2}$c,由2a+2b+$\sqrt{2}$c=6$\sqrt{2}$,即2(a+b)+$\sqrt{2}$c=6$\sqrt{2}$,推出c=2,推出a2+b2=c2=4,a+b=2$\sqrt{2}$,由(a+b)2=a2+2ab+b2,可得ab=2,由此即可解决问题.
解答 (1)证明:由题意,得
△=($\sqrt{2}$c)2-4ab=2c2-4ab,
∵a2+b2=c2,
∴2c2-4ab=2(a2+b2)-4ab=2(a-b)2≥0,
即△≥0,
∴关于x的“勾系一元二次方程”ax2+$\sqrt{2}$cx+b=0必有实数根
(2)解:当x=-1时,有a-$\sqrt{2}$c+b=0,即a+b=$\sqrt{2}$c,
∵2a+2b+$\sqrt{2}$c=6$\sqrt{2}$,即2(a+b)+$\sqrt{2}$c=6$\sqrt{2}$,
∴3$\sqrt{2}$c=6$\sqrt{2}$,
∴c=2,
∴a2+b2=c2=4,a+b=2$\sqrt{2}$,
∵(a+b)2=a2+2ab+b2,
∴ab=2,
∴S△ABC=$\frac{1}{2}$ab=1.
点评 本题考查勾股定理的应用、一元二次方程的根与系数的关系、完全平方公式等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{125}$ | B. | -125 | C. | $\frac{1}{125}$ | D. | 125 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两点之间线段最短 | |
| B. | 三角形的内心是这个三角形三边垂直平分线的交点 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 五边形的外角和为540度 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5×10-7 | B. | 2.5×10-6 | C. | 0.25×10-5 | D. | 2.5×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 137×108 | B. | 1.37×109 | C. | 1.37×1010 | D. | 0.137×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com