
【题目】在△ABC中,∠ACB=90°,BC=AC=2,将△ABC绕点A顺时针方向旋转α角(0°<α<180°)至△AB'C'的位置.
问题探究:
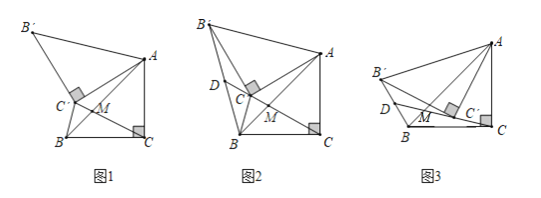
(1)如图1,当旋转角为60°时,连接C'C与AB交于点M,则C'C= ,![]() .
.
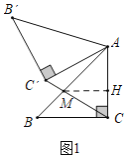
(2)如图2,在(1)条件下,连接BB',延长CC'交BB'于点D,求CD的长.
问题解决:
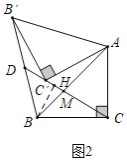
(3)如图3,在旋转的过程中,连线CC'、BB',CC'所在直线交BB'于点D,那么CD的长有没有最大值?如果有,求出CD的最大值:如果没有,请说明理由.
【答案】(1)2,2![]() ﹣2;(2)1+
﹣2;(2)1+![]() ;(3)
;(3)![]() 的长有最大值, 2
的长有最大值, 2![]() .
.
【解析】
(1)如图1中,证明![]() 是等边三角形即可解决问题.作
是等边三角形即可解决问题.作![]() 于
于![]() ,设
,设![]() ,构建方程求出
,构建方程求出![]() ,再根据
,再根据![]() 即可求出
即可求出![]() .
.
(2)如图2中,作![]() 于
于![]() .想办法证明
.想办法证明![]() ,
,![]() ,即可解决问题.
,即可解决问题.
(3)![]() 的值有最大值.取
的值有最大值.取![]() 的中点
的中点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() .说明点
.说明点![]() 的运动轨迹是
的运动轨迹是![]() ,即可解决问题.
,即可解决问题.
解:(1)如图1中,作![]() 于
于![]() .
.
当旋转角为![]() 时,
时,![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为2,![]() .
.
(2)如图2中,作![]() 于
于![]() .
.
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(3)![]() 的长有最大值.
的长有最大值.
理由:如图3中,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() △
△![]() △
△![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
取![]() 的中点
的中点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 的运动轨迹是
的运动轨迹是![]() ,当
,当![]() 时,
时,![]() 的值最大,此时
的值最大,此时![]() .
.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则小明打开走廊灯的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
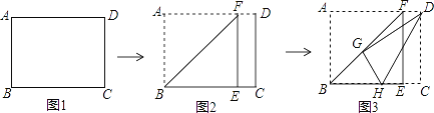
【题目】如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
①AF的长为10;②△BGH的周长为18;③![]() =
=![]() ;④GH的长为5,
;④GH的长为5,
其中正确的结论有________.(写出所有正确结论的番号)
查看答案和解析>>
科目:初中数学 来源: 题型:
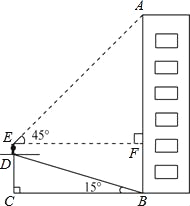
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
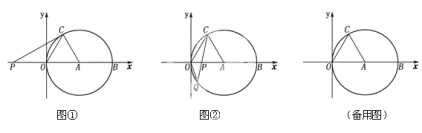
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
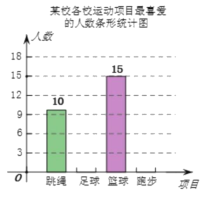
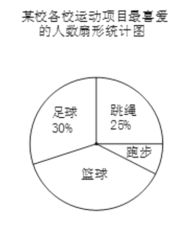
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,“篮球”部分所对应的圆心角度数为__ ;
(4)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com