

���� ������ĿҪ�������ACΪֱ�DZߵĵ���ֱ�������Σ���AC=BC����C=90�㣬Ȼ���ɹ��ɶ������AB�ij��������������ĵ���ֱ�������ε��ܳ����ɣ�
��� �⣺����ͼ1���ӳ�BC��D��ʹAB=AD������AD����AB=AD=10ʱ������CD=CB=6�á�ABD���ܳ�Ϊ32m��
����ͼ2����AB=BD=10ʱ������CD=4��
�ɹ��ɶ����ã�AD=4$\sqrt{5}$�á�ABD���ܳ�Ϊ��20+4$\sqrt{5}$��m��
����ͼ3����ABΪ��ʱ����AD=BD=x����CD=x-6���ɹ��ɶ����ã�x=$\frac{25}{3}$��
�á�ABD���ܳ�Ϊ$\frac{80}{3}$m�� 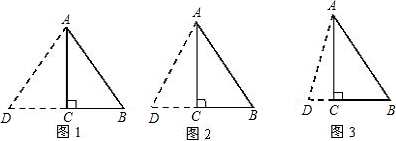
���� ������Ҫ����Թ��ɶ��������������ε����ʵ�֪ʶ�����������գ���ͨ������������������ε���������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC�ա�ADE����D��BC�ϣ���ABC=60�㣬��C=45�㣬���ADE�ɿ������ɡ�ABC�ض���A��ʱ����ת60�ȵõ��ģ�
��ͼ����֪��ABC�ա�ADE����D��BC�ϣ���ABC=60�㣬��C=45�㣬���ADE�ɿ������ɡ�ABC�ض���A��ʱ����ת60�ȵõ��ģ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x-1}{y-1}$ | B�� | $\frac{x+1}{y+1}$ | C�� | $\frac{x^2}{y^3}$ | D�� | $\frac{x}{x+y}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 8$\sqrt{3}$ | C�� | 2$+\sqrt{3}$ | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com