(1)证明:∵△=a
2-4(a-2)=a
2-4a+8=(a-2)
2+4>0,
∴不论a为何实数,此方程总有两个不相等的实数根.
(2)解:设x
1、x
2是y=x
2+ax+a-2=0的两个根,则x
1+x
2=-a,x
1•x
2=a-2,
∵两交点的距离是

,
∴|x
1-x
2|=
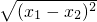
=

.
即:(x
1-x
2)
2=13,
变形为:(x
1+x
2)
2-4x
1•x
2=13,
∴(-a)
2-4(a-2)=13,
整理得:(a-5)(a+1)=0,
解方程得:a=5或-1,
又∵a<0,
∴a=-1,
∴此二次函数的解析式为y=x
2-x-3.
(3)解:设点P的坐标为(x
0,y
0),
∵函数图象与x轴的两个交点间的距离等于

,
∴AB=

,
∴S
△PAB=

AB•|y
0|=
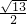
,
∴
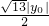
=
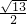
即:|y
0|=3,
解得:y
0=±3,
当y
0=3时,x
02-x
0-3=3,即(x
0-3)(x
0+2)=0,
解此方程得:x
0=-2或3,
当y
0=-3时,x
02-x
0-3=-3,即x
0(x
0-1)=0,
解此方程得:x
0=0或1,
综上所述,所以存在这样的P点,P点坐标是(-2,3)或(3,3)或(0,-3)或(1,-3).
分析:(1)由△=a
2-4(a-2)=a
2-4a+8=(a-2)
2+4>0,即可判定不论a为何实数,此方程总有两个不相等的实数根;
(2)首先设x
1、x
2是y=x
2+ax+a-2=0的两个根,则x
1+x
2=-a,x
1•x
2=a-2,由两交点的距离是

,可得:(x
1-x
2)
2=13,即可得(x
1+x
2)
2-4x
1•x
2=13,继而求得a的值;
(3)首先设点P的坐标为(x
0,y
0),由AB=

,△PAB的面积为
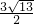
,即可求得y
0的值,继而求得P点坐标.
点评:此题属于二次函数的综合题,考查了根的判别式、根与系数的关系、两点间的距离公式以及点与二次函数的关系.此题难度较大,注意掌握方程思想的应用.

 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;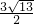 ?若存在求出P点坐标,若不存在请说明理由.
?若存在求出P点坐标,若不存在请说明理由. ,
,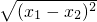 =
= .
. ,
, ,
, AB•|y0|=
AB•|y0|=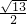 ,
,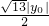 =
=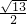
 ,可得:(x1-x2)2=13,即可得(x1+x2)2-4x1•x2=13,继而求得a的值;
,可得:(x1-x2)2=13,即可得(x1+x2)2-4x1•x2=13,继而求得a的值; ,△PAB的面积为
,△PAB的面积为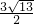 ,即可求得y0的值,继而求得P点坐标.
,即可求得y0的值,继而求得P点坐标.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案