
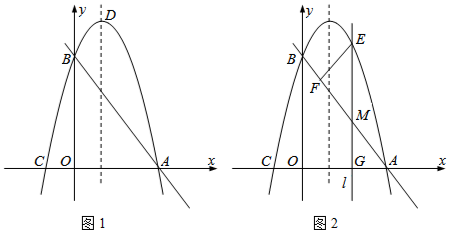
���� ��1�������A��B���꣬���ô���ϵ��������A��B��C������������ʽ������ö��κ����Ľ���ʽ��
��2������ͼ�Σ��ҳ�P���λ�ã����ɽ��⣻
��3������m��ʾ�߶�EM�ij��ȣ������EM��EF�ij��ȹ�ϵ���ɽ��⣮
��� �⣺��1��ֱ��y=-2x+4��x�ᡢy��Ľ���A��B������ֱ���A��2��0����B��0��4����
������ĺ�������ʽΪy=ax2+bx+c���ѵ�A��2��0����B��0��4����C��-1��0�������
$\left\{\begin{array}{l}{4a+2b+c=0}\\{a-b+c=0}\\{c=4}\end{array}\right.$�����a=-2��b=2��c=4��
��y=-2x2+2x+4��
��2�����ڣ�����ͼ�Σ������߽���ʽΪy=-2x2+2x+4��
�ඥ��D������Ϊ��$\frac{1}{2}$��$\frac{9}{2}$����
��BD=$\frac{\sqrt{2}}{2}$��
����ͼ�٣���ʱBD=DP��P������Ϊ��$\frac{1}{2}$��$\frac{9}{2}$+$\frac{\sqrt{2}}{2}$����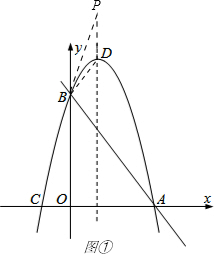
����ͼ�ڣ���ʱBD=DP��P������Ϊ��$\frac{1}{2}$��$\frac{9}{2}$-$\frac{\sqrt{2}}{2}$����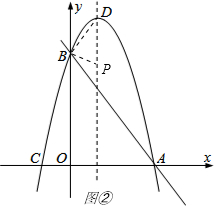
����ͼ�ۣ���ʱBD=BP��P������Ϊ��$\frac{1}{2}$��$\frac{7}{2}$����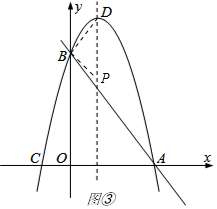 ��
��
��3�����������M��m��-2m+4����E��m��-2m2+2m+4����
��EM=-2m2+2m+4-��-2m+4��=-2m2+4m��
����Rt��AOB�У����ݹ��ɶ�������AB=$\sqrt{{OA}^{2}{+OB}^{2}}$=2$\sqrt{5}$��
��$\frac{OA}{AB}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$��
��y���EG��
���AOB�ס�AGM��
��$\frac{AG}{AM}$=$\frac{OA}{AB}$��
���ڡ�EMF�͡�AMG�У�$\left\{\begin{array}{l}{��AGM=��EFM=90��}\\{��AMG=��EMF}\end{array}\right.$��
���EMF�ס�AMG��
��$\frac{AG}{AM}$=$\frac{EF}{EM}$��
��$\frac{EF}{EM}$=$\frac{AG}{AM}$=$\frac{OA}{AB}$=$\frac{\sqrt{5}}{5}$��
��EF=$\frac{\sqrt{5}}{5}$EM=$\frac{\sqrt{5}}{5}$��-2m2+4m��=-$\frac{2\sqrt{5}}{5}$��m-1��2+$\frac{2\sqrt{5}}{5}$��
�൱m=1ʱ���߶�EF�ij������ֵΪ$\frac{2\sqrt{5}}{5}$��
���� ���⿼���˴���ϵ���������ʽ���������˶��κ������ֵ����⣻Ҫ���������ν�ϵ�˼��Ѵ����ͼ���ͼ�ν����������Ҫע�������ֵ���Խ����ڶ��κ�����


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
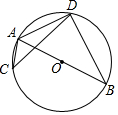 ��ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O��λ��AB�������㣮�����ĸ����У�һ�����ACD����Ľ��ǣ�������
��ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O��λ��AB�������㣮�����ĸ����У�һ�����ACD����Ľ��ǣ�������| A�� | ��ADC | B�� | ��ABD | C�� | ��BAC | D�� | ��BAD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
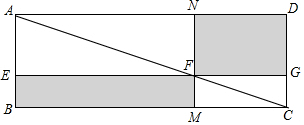 ��ѧ�����Ŀ�Ժʿ�dz����ӹŴ���ѧ�Ҽ�������ġ��ӳ����ζԽ�������һ���������ֱ�ƽ�������ڱߵ�ֱ�ߣ��������������������ȣ���ͼ��ʾ������һ���ۣ�������һ���۳��������á������ಹ��ԭ����ԭ�ˡ������㾭�������֤��
��ѧ�����Ŀ�Ժʿ�dz����ӹŴ���ѧ�Ҽ�������ġ��ӳ����ζԽ�������һ���������ֱ�ƽ�������ڱߵ�ֱ�ߣ��������������������ȣ���ͼ��ʾ������һ���ۣ�������һ���۳��������á������ಹ��ԭ����ԭ�ˡ������㾭�������֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | ���ӻ� | ϴ�»� |
| ���ۣ�Ԫ/̨�� | 1800 | 1500 |
| �ۼۣ�Ԫ/̨�� | 2000 | 1600 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��+2 | B�� | ��-3����2 | C�� | ��-3��2 | D�� | -23 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com