
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒.
(1) 当t=1时,求△ACP的面积
(2) t为何值时,线段AP是∠CAB的平分线?
(3) 请利用备用图2继续探索:当t为何值时,△ACP是以AC为腰的等腰三角形?
【答案】(1).6;(2).1.5;(3)3,6或5.4
【解析】试题分析:(1)把t=1代入得出CP=2,利用三角形的面积进行解答即可;
(2)过P作PE⊥AB,设CP=2t,根据角平分线的性质和勾股定理进行解答即可;
(3)根据AC=CP,利用等腰直角三角形的性质解答即可.
试题解析:
(1)把t=1得出CP=2,所以△ACP的面积=![]() ×2×6=6cm2;
×2×6=6cm2;
(2)过P作PE⊥AB,如图1: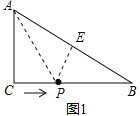
CP=2t,BP=(8-2t)cm,AE=AC=6cm,PE=CP=2t,BE=10-6=4,
可得:(8-2t)2=(2t)2-42
解得:t=![]() s;
s;
(3)如图2,3,4: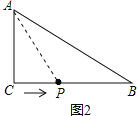
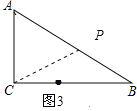
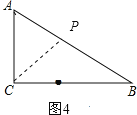
因为△ACP是以AC为腰的等腰三角形,
当AC=CP=6时,t1=6÷2=3s;
当AC=CP=6时,t2=4+![]() =
=![]() s;
s;
当AC=AP=6时,t3=4+2=6s.
所以当t为3,6, ![]() 时,△ACP是以AC为腰的等腰三角形.
时,△ACP是以AC为腰的等腰三角形.


科目:初中数学 来源: 题型:
【题目】(2016山东省聊城市第11题)如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )

A.115° B.120° C.130° D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下框中的题目.

小敏与同桌小聪讨论后,进行了如下解答:
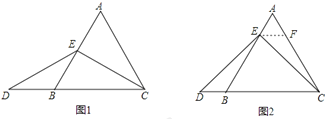
(1)特殊情况探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE__________DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE__________DB(填“>”,“<”或“=”).理由如下:
如图2,过点E作EF∥BC,交AC于点F,(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
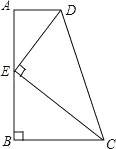
A.CE=![]() DE B.CE=
DE B.CE=![]() DE C.CE=3DE D.CE=2DE
DE C.CE=3DE D.CE=2DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com