
���� ��1�����ݶ�Ԫһ�η��̵Ľ�ö���������ɣ�
��2����������ó�x-3=6��3��2��1��������ɣ�
��3�������y��ֵ���������k��ֵ��
��� �⣺��1������3x+2y=8����������Ϊ$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$��
�ʴ�Ϊ$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$��
��2����������9��6��5��4����4����
��ѡB��
��3��$\left\{\begin{array}{l}{x+2y=9��}\\{2x+ky=10��}\end{array}\right.$
�١�2-�ڵã���4-k��y=8��
��ã�y=$\frac{8}{4-k}$��
��x��y����������k��������
4-k=1��2��4��8��
��k=3��2��0��-4��
��k=3ʱ��x��������������k=2��0��-4��
���� ���⿼���˶�Ԫһ�η�����Ľ⣬��Ԫһ�η��̵Ľ��Ӧ�ã����������֪ʶ�����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.8 | B�� | 0.75 | C�� | 0.6 | D�� | 0.48 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2 | B�� | 2 | C�� | -2 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
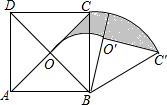 ��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����OBC�Ƶ�B˳ʱ����ת60��õ���0��BC�䣬��AB=2����ͼ����Ӱ���ֵ������ $\frac{��}{3}$��
��ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����OBC�Ƶ�B˳ʱ����ת60��õ���0��BC�䣬��AB=2����ͼ����Ӱ���ֵ������ $\frac{��}{3}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com