
分析 (1)①根据3x2-5x+1=0,等式两边同除以x即可解答本题;
②根据①中的结果,两边同时平方,再化简即可解答本题;
(2)先化简所求式子,再根据3xm+1-2xn-1+xn是关于x的二次多项式,可以求得m、n的值,然后代入化简后的式子即可解答本题.
解答 解:(1)①∵3x2-5x+1=0,
∴3x-5+$\frac{1}{x}$=0,
∴3x+$\frac{1}{x}$=5;
②∵3x+$\frac{1}{x}$=5
∴$(3x+\frac{1}{x})^{2}=25$,
∴$9{x}^{2}+6+\frac{1}{{x}^{2}}$=25,
∴$9{x}^{2}+\frac{1}{{x}^{2}}$=19;
(2)3(m-n)2-4(n-m)2-(m-n)3+2(n-m)3
=-(m-n)2+3(n-m)3
∵3xm+1-2xn-1+xn是关于x的二次多项式,
∴$\left\{\begin{array}{l}{m+1=2}\\{n=2}\end{array}\right.$或$\left\{\begin{array}{l}{m+1=2}\\{n=1}\end{array}\right.$或$\left\{\begin{array}{l}{m+1=1}\\{n=2}\end{array}\right.$或$\left\{\begin{array}{l}{m+1=0}\\{n=2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{m=1}\\{n=2}\end{array}\right.$或$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$或$\left\{\begin{array}{l}{m=0}\\{n=2}\end{array}\right.$或$\left\{\begin{array}{l}{m=-1}\\{n=2}\end{array}\right.$,
∴当m=1,n=2时,原式=-(1-2)2+3(2-1)3=-1+3=2;
当m=1,n=1时,原式=-(1-1)2+3(1-1)3=0;
当m=0,n=2时,原式=-(0-2)2+3(2-0)3=-4+24=20;
当m=-1,n=2时,原式=-(-1-2)2+3(2+1)3=-9+81=72.
点评 本题考查分式的化简求值、多项式、完全平方公式,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
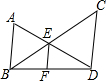 已知,如图,AB∥EF∥CD,E为AD,BC的交点,点B,F,D在一条直线上,设AB=a,CD=b,EF=c,猜想:a,b,c之间有什么关系?并证明你的猜想.
已知,如图,AB∥EF∥CD,E为AD,BC的交点,点B,F,D在一条直线上,设AB=a,CD=b,EF=c,猜想:a,b,c之间有什么关系?并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠C=90°,AC=BC,将∠A沿直线MN折叠,使点A落在BC边上的点D处,若∠MDC=45°,则S△MND:S△BDN的值是$\sqrt{2}$:2.
如图,在Rt△ABC中,∠C=90°,AC=BC,将∠A沿直线MN折叠,使点A落在BC边上的点D处,若∠MDC=45°,则S△MND:S△BDN的值是$\sqrt{2}$:2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | (1)(2)(4) | B. | (4)(2)(3) | C. | (1)(2)(3) | D. | (4)(1)(2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
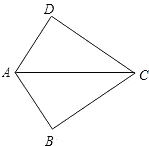 如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | CB=CD | B. | ∠BAC=∠DAC | C. | ∠BCA=∠DCA | D. | ∠B=∠D=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com