
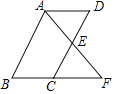
【题目】如图,点E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若AB=8,BC=5,则EF的长为 时,AB⊥AF.
【答案】(1)见解析;(2)3
【解析】
(1)利用中点定义可得DE=CE,再用平行四边形的性质可得∠D=∠DCF,然后可证明△ADE≌△FCE;
(2)根据平行四边形的性质可得CE=4,CF=5,然后利用勾股定理可得EF的长.
(1)证明:∵E是边CD的中点,
∴DE=CE,
∵四边形ABCD是平行四边形,
∴AD∥BF,
∴∠D=∠DCF,
在△ADE和△FCE中
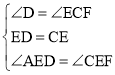 ,
,
∴△ADE≌△FCE(ASA);
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD=8,CD=AD=5,AB∥CD,
∵△ADE≌△FCE,
∴AD=CF=5,
∵E为CD中点,
∴CE=4,
∵AB⊥AF,AB∥CD,
∴CE⊥EF,
∴EF=3,
故答案为:3.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.

(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,表示的数分别是-4、-2、3,请回答:
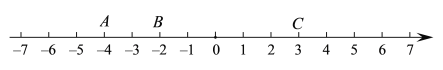
(1)若C、B两点的距离与A、B两点距离相等,则需将点C向左移动________个单位;
(2)若移动A、B、C三点中的两点,使三个点表示的数相同,移动方法有________种,其中移动所走的距离之和最小的是________个单位;
(3)若在B处有一小青蛙,一步跳一个单位长,小青蛙第一次先向左跳一步,第2次向右跳3步,第3次向再向左跳5步,第4次再向右跳7步……,按此规律继续下去,那么跳第100次时落脚点表示的数是________;
(4)若有两只小青蛙M、N,它们在数轴上的点表示的数分别为整数x、y,且|x-2|+|y+3|=2,求两只青蛙M、N之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() +
+![]() =0,请回答问题:
=0,请回答问题:
(1)请直接写出a、b、c的值;
(2)数轴上a、b、c所对应的点分别为A、B、C,点M是A、B之间的一个动点,其对应的数为m,请化简![]() (请写出化简过程);
(请写出化简过程);
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动.若点A以每秒1个单位长度的速度向左运动.同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3![]() ,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与ABCD的一边垂直时,DM的长为_____.
,BC=10,∠A=45°,点E是边AD上一动点,将△AEB沿直线BE折叠,得到△FEB,设BF与AD交于点M,当BF与ABCD的一边垂直时,DM的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB的右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,则障碍物B,C两点间的距离是( )

A. 50m B. (70-10![]() )m C. (70+10
)m C. (70+10![]() )m D.
)m D. 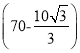 m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应集合内:﹣2,![]() ,4,1.1010010001,
,4,1.1010010001,![]() ,π,0.3%,
,π,0.3%,![]() ,﹣|﹣3|,(﹣1)2012
,﹣|﹣3|,(﹣1)2012
整数集合:[_____…];
分数集合:[_____…];
无理数集合:[_____…];
正数集合:[_____…].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据图中信息解答下列问题:
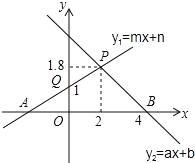
(1)关于x的不等式ax+b>0的解集是 ;
(2)关于x的不等式mx+n<1的解集是 ;
(3)当x满足 的条件时,y1y2;
(4)当x满足 的条件时,0<y2<y1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC内接于⊙O,P是![]() 上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
上任一点(点P不与点A、B重合),连AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)填空:∠APC=____ 度,∠BPC=____度;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求梯形PBCM的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com