
分析 首先根据题意画出三种情况的图形,再根据三角形的面积公式求出答案即可.
解答 解:如图四边形ABCD是矩形,AD=18cm,AB=16cm;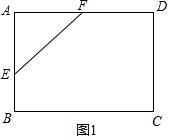
本题可分三种情况:
①如图1:△AEF中,AE=AF=10cm;
S△AEF=$\frac{1}{2}$•AE•AF=50cm2;
②如图2:△AGH中,AG=GH=10cm;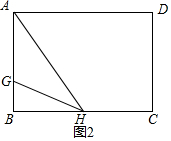
在Rt△BGH中,BG=AB-AG=16-10=6cm;
根据勾股定理有:BH=8cm;
∴S△AGH=$\frac{1}{2}$AG•BH=$\frac{1}{2}$×8×10=40cm2;
③如图3:△AMN中,AM=MN=10cm;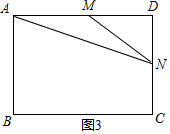
在Rt△DMN中,MD=AD-AM=18-10=8cm;
根据勾股定理有DN=6cm;
∴S△AMN=$\frac{1}{2}$AM•DN=$\frac{1}{2}$×10×6=30cm2.
故答案为30或40或50.
点评 本题主要考查了等腰三角形的性质、矩形的性质、勾股定理等知识,解题的关键在于能够进行正确的讨论.


科目:初中数学 来源: 题型:解答题
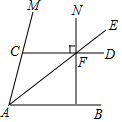 如图,AB∥CD,AE平分∠MAB交CD于点F,NF⊥CD,垂足为点F.
如图,AB∥CD,AE平分∠MAB交CD于点F,NF⊥CD,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
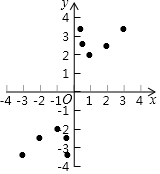 某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:
某班“数学兴趣小组”对函数y=x+$\frac{1}{x}$的图象和性质进行了探究,探究过程如下,请补充完整:| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | -$\frac{10}{3}$ | -$\frac{5}{2}$ | -2 | -$\frac{5}{2}$ | -$\frac{10}{3}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
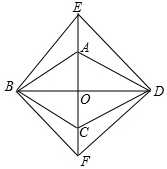 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD,AB=3,BC=4,点P是边AD的上一点,将△ABP沿着直线BP翻折,点A的对应点为点A′.若点A′到B点的距离等于它到CD边的距离,则AP=9-6$\sqrt{2}$.
如图,已知矩形ABCD,AB=3,BC=4,点P是边AD的上一点,将△ABP沿着直线BP翻折,点A的对应点为点A′.若点A′到B点的距离等于它到CD边的距离,则AP=9-6$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
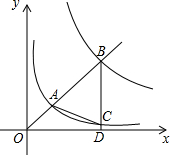 如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.
如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=$\frac{1}{x}$和y=$\frac{9}{x}$在第一象限的图象于点A,B,过点B作 BD⊥x轴于点D,交y=$\frac{1}{x}$的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是$\frac{3\sqrt{7}}{7}$或$\frac{\sqrt{15}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com