
解:(1)∵反比例函数y=

(m≠0)的图象经过点A(-2,6),
∴m=-2×6=-12,
∴m的值为-12;
(2)由(1)得反比例函数的解析式为y=-

,
过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,
∴∠BEC=∠ADC=90°,
又∵∠BCE=∠ACD,
∴△BEC∽△ADC,
∴

=

=

,
∵AD=6,
∴BE=2,
∴点B的纵坐标为2,
又∵点B在反比例函数y=-

的图象上,
∴点B的横坐标为x=-6,
则点B的坐标为(-6,2).
分析:(1)将A坐标代入反比例解析式中计算,即可求出m的值;
(2)由(1)求出的m值,确定出反比例解析式,过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,可得出一对直角相等,再由一对公共角,利用两对对应角相等的两三角形相似,得到三角形BEC与三角形ADC相似,由相似得比例,根据已知BC与AC的比值,及AD的长求出CE的长,即为B的横坐标,将B横坐标代入反比例解析式中求出对应y的值,即为B的纵坐标,即可确定出B的坐标.
点评:此题考查了反比例函数综合题,涉及的知识有:相似三角形的判定与性质,坐标与图形性质,以及待定系数法的运用,熟练掌握待定系数法是解本题的关键.

 已知反比例函数
已知反比例函数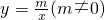 的图象经过点A(-2,6).
的图象经过点A(-2,6). 的图象交于点B,与x轴交于点C,且
的图象交于点B,与x轴交于点C,且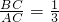 ,求点B的坐标.
,求点B的坐标. 解:(1)∵反比例函数y=
解:(1)∵反比例函数y= (m≠0)的图象经过点A(-2,6),
(m≠0)的图象经过点A(-2,6), ,
, =
= =
= ,
, 的图象上,
的图象上,
