

分析 (1)利用待定系数法直接求出抛物线解析式;
(2)由折叠的性质得出∠BAF=∠B'AF,∠ABF=∠AB'F,再用直角三角形的两锐角互余转化即可得出∠DAC=45°,即可;
(3)由折叠的性质得出AB'进而得出OB'即可得出点B'的坐标,再用角平分线定理得出点F的坐标,同样的道理得出点G的坐标,进而得出tan∠OBG=$\frac{1}{4}$,即可得出点E的坐标,用待定系数法求出直线AE解析式,最后直线AE解析式和抛物线解析式联立即可确定出点P的坐标.
解答 解:(1)∵抛物线y=ax2+bx+3与x轴交于点 A(-4,0)和点B($\frac{9}{2}$,0);
∴$\left\{\begin{array}{l}{16a-4b+c=0}\\{\frac{81}{4}a+\frac{9}{2}b+c=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{1}{6}}\\{b=\frac{1}{12}}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{6}$x2+$\frac{1}{12}$x+3,
(2)∵将△ABF沿直线AF翻折得到△AFB′,
∴∠BAF=∠B'AF,∠ABF=∠AB'F,
∵∠ABF=2∠PAB,
∴∠AB'F=2∠PAB,
∵∠AB'F+∠B'AO=90°,
∴2∠PAB+∠B'AF+∠BAF=2∠PAB+2∠BAF=90°,
∴∠PAB+∠BAF=45°,
∴∠CAF=45°,
∵CD⊥AC,
∴∠ACD=90°,
∴∠ADC=45°.
(3)如图3,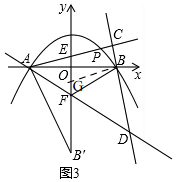 当直线m与y轴重合时,
当直线m与y轴重合时,
由折叠知,BF=B'F,AB'=AB=$\frac{9}{2}$+4=$\frac{17}{2}$,
在Rt△AOB'中,OB'=$\sqrt{AB{'}^{2}-O{A}^{2}}$=$\frac{15}{2}$,
∴B'(0,-$\frac{15}{2}$)
设F(0,m),
∴OF=-m,B'F=m+$\frac{15}{2}$,
∵∠B'AF=∠OAF,
∴$\frac{OA}{AB'}=\frac{OF}{B'F}$,
∴$\frac{4}{\frac{17}{2}}=\frac{-n}{m+\frac{15}{2}}$,
∴m=-$\frac{12}{5}$,
∴F(0,-$\frac{12}{5}$),
∴BF=B'F=-$\frac{12}{5}$+$\frac{15}{2}$=$\frac{51}{10}$,
过点B作∠ABF的角平分线交y轴于G,
∴∠OBG=∠FBG=$\frac{1}{2}$∠ABF=∠BAP,
设G(0,n),
∴OG=-n,FG=n+$\frac{12}{5}$,
∵∠OBG=∠FBG,
∴$\frac{OB}{BF}=\frac{OG}{FG}$,
∴$\frac{\frac{9}{2}}{\frac{51}{10}}=\frac{-n}{n+\frac{12}{5}}$,
∴n=-$\frac{9}{8}$,
∴G(0,-$\frac{9}{8}$),
∴OG=$\frac{9}{8}$,
∴tan∠OBG=$\frac{OG}{OB}$=$\frac{\frac{9}{8}}{\frac{9}{2}}$=$\frac{1}{4}$,
∵∠BAP=∠OBG,
∴tan∠BAP=$\frac{OE}{OA}$=$\frac{OE}{4}$=$\frac{1}{4}$,
∴OE=1,
∴E(0,1),
∵A(-4,0),
∴直线AE的解析式为y=$\frac{1}{4}$x+1①,
∵点P是抛物线y=-$\frac{1}{6}$x2+$\frac{1}{12}$x+3②上,
联立①②解得,$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=3}\\{y=\frac{7}{4}}\end{array}\right.$,
∴P(3,$\frac{7}{4}$).
点评 此题是二次函数综合题,主要考查了待定系数法,直角三角形的性质,锐角三角函数,折叠的性质,角平分线定理,用角平分线定理得出OF和OG是解本题的关键,作出辅助线是解本题的难点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
【背景介绍】勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
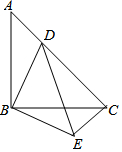 等腰Rt△ABC中,BA=BC,∠ABC=90°,将△ABD绕点B顺时针旋转90°后,得到△CBE.若AB=6,CD=2AD,求DE的长.
等腰Rt△ABC中,BA=BC,∠ABC=90°,将△ABD绕点B顺时针旋转90°后,得到△CBE.若AB=6,CD=2AD,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
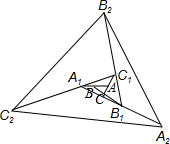 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2016次操作后△A2016B2016C2016的面积为72016.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2016次操作后△A2016B2016C2016的面积为72016.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.
等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com