

分析 (1)由∠DFC=90°,∠C=30°,证出DF=2t=AE;
(2)当四边形BEDF是矩形时,△DEF为直角三角形且∠EDF=90°,求出t的值即可;
(3)先证明四边形AEFD为平行四边形.得出AB=30,AD=AC-DC=60-4t,若△DEF为等边三角形,则四边形AEFD为菱形,得出AE=AD,2t=60-4t,求出t的值即可.
解答 (1)证明:在△DFC中,∠DFC=90°,∠C=30°,DC=4t,
∴DF=$\frac{1}{2}$CD=2t.
又∵AE=2t,
∴AE=DF;
(2)∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE.即60-4t=4t,
∴t=$\frac{15}{2}$.
故答案是:$\frac{15}{2}$;
(3)能;
理由如下:
∵AB⊥BC,DF⊥BC,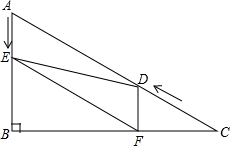
∴AE∥DF.
又AE=DF,
∴四边形AEFD为平行四边形.
∵∠C=30°,AC=60,
∴AB=30,
∴AD=AC-DC=6-2t,
若平行四边形AEFD为菱形,则AE=AD,
∴2t=60-4t,
∴t=10;
即当t=10时,四边形AEFD能够成为菱形.
点评 本题是四边形综合题,主要考查了平行四边形、菱形、矩形的判定与性质以及锐角三角函数的知识;考查学生综合运用定理进行推理和计算的能力.


科目:初中数学 来源: 题型:解答题
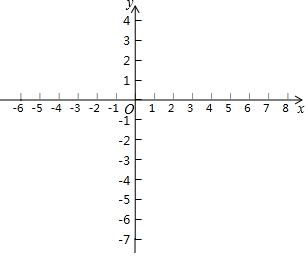 已知:直线y=-$\frac{1}{2}$x+2与x轴交于点A,直线y=3x-1与x轴交于点B,与y轴交于点C,两直线交于点D
已知:直线y=-$\frac{1}{2}$x+2与x轴交于点A,直线y=3x-1与x轴交于点B,与y轴交于点C,两直线交于点D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com