
| ������ | Ƶ�� | Ƶ�� |
| 72������ | 368 | 0.2 |
| 72----80�� | 460 | 0.25 |
| 81----95�� | 644 | 0.35 |
| 96----108�� | 184 | 0.2 |
| 109----119�� | 130 | |
| 120�� | 54 |
���� ����72�����µ���������Ƶ�ʿɵ���������
����81--95�ֵ�Ƶ��=1-0.2-0.25-0.2�������������ɼ����81--95�ֵ�Ƶ����Ȼ������5�����о��꼶ѧ�����������ֱ��ȥ�������ε�Ƶ�����ɵõ�109---119�ֵ�Ƶ����
�۸��ݸ��ʵĸ������������ȡһ�ˣ�ǡ����108�����ϵĸ��ʣ�
��� �⣺��1����5�����о��꼶ѧ����������=368��0.2=1840�ˣ�
��2����81----95�ֵ�Ƶ��Ϊ1-��0.2+0.25+0.2��=0.35��
��81----95�ֵ�Ƶ��Ϊ1840��0.35=644�ˣ�
��109----119�ֵ�Ƶ��Ϊ1840-��368+460+644+184+54��=130��
�ʴ�Ϊ��644��0.35��130��
�������ȡһ�ˣ�ǡ���ǻ��108�����ϵĸ���=$\frac{130+54}{1840}$=$\frac{1}{10}$��
���� ���⿼����Ƶ����Ƶ�ʡ����ʵ����֪ʶ���������Ĺؼ��Ǹ�����Ŀ�ṩ����Ϣ���мӹ������������������һ�����Ϣ��������ѧ���ǵ����⡢�ӹ���Ϣ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5�� | B�� | 6�� | C�� | 7�� | D�� | 8�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
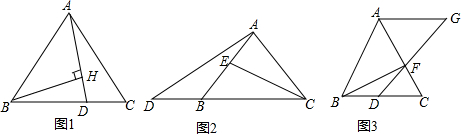
 ��ͼ����֪������ABCD�ı߳�Ϊ2����DCΪ��������������������DEC������AE����AEΪ����������AEF��ʹ��EA=EF���ҡ�DEC=��AEF��
��ͼ����֪������ABCD�ı߳�Ϊ2����DCΪ��������������������DEC������AE����AEΪ����������AEF��ʹ��EA=EF���ҡ�DEC=��AEF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com