
分析 分两种情形画出图形分别求解即可.
解答 解:如图1中,当点E在线段BC上时.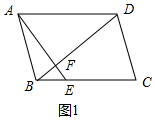
∵四边形ABCD是平行四边形,EC=3BE,
∴AD=BC,AD∥BC,
∴BE:AD=BF:DF=EF:AF=1:4,△ADF∽△EBF,
∴S△BEF:S△ABF=1:4,S△BEF:S△ADF=1:16,∵S△BEF=1,
∴S△ABF=4,S△ADF=16,
∴S△ABD=4+16=20,
∴平行四边形ABCD的面积=2S△ABD=40.
如图2中,当点E在CB的延长线上时.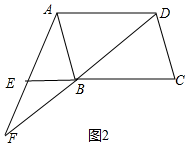
∵EB∥AD,EC=3EB,
∴EB:AD=FE:FA=BF:BD=1:2,
∴EF=AE,BF=BD,
∴S△AEB=1,S△ABD=S△ABF=2,
∴平行四边形ABCD的面积=2S△ABD=4.
综上所述,平行四边形ABCD的面积为40或4.
故答案为40或4.
点评 本题考查平行四边形的性质,平行线分线段成比例定理,相似三角形的判定和性质,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,掌握同高异底的两个三角形的面积比等于底的比,属于中考常考题型.


科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
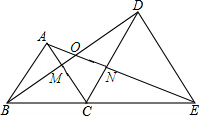 如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.
如图,B,C,E三点在一条直线上,△ABC和△DCE均为等边三角形,BD与AC交于点M,AE与CD交于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com