
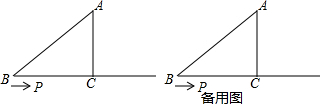
分析 (1)首先直接根据勾股定理求出BC的长度,再分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
(2当△ABP为等腰三角形时,分三种情况:①当AB=BP时;②当AB=AP时;③当BP=AP时,分别求出BP的长度,继而可求得t值.
解答 (1)解:∵∠C=90°,AB=5cm,AC=3cm,
∴BC=4 cm.
①当∠APB为直角时,点P与点C重合,BP=BC=4 cm,
∴t=4.
②当∠BAP为直角时,BP=t cm,CP=(t-4)cm,AC=3 cm,
在Rt△ACP中,AP2=32+(t-4)2,
在Rt△BAP中,AB2+AP2=BP2,
∴52+[32+(t-4)2]=t2,
解得t=$\frac{25}{4}$.
综上,当△ABP为直角三角形时,t=4或$\frac{25}{4}$.
(2)解:①当BP=BA=5时,∴t=5.
②当AB=AP时,BP=2BC=8cm,∴t=8.
③当PB=PA时,PB=PA=t cm,CP=(4-t)cm,AC=3 cm,
在Rt△ACP中,AP2=AC2+CP2,
∴t2=32+(4-t)2,解得t=$\frac{25}{8}$.
综上,当△ABP为等腰三角形时,t=5或8或$\frac{25}{8}$.
点评 本题考查了勾股定理以及等腰三角形的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
 如图,半径为1的圆在数轴上滚动,开始在数轴上点A(称圆与数轴的切点)处,向左滚动一周至点B处,若点A对应的数是3,则点B对应的数是( )
如图,半径为1的圆在数轴上滚动,开始在数轴上点A(称圆与数轴的切点)处,向左滚动一周至点B处,若点A对应的数是3,则点B对应的数是( )| A. | 3-π | B. | 2π-3 | C. | π-3 | D. | 3-2π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5349×103 | B. | 5.349×103 | C. | 5.349×106 | D. | 5.349×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{15}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com