
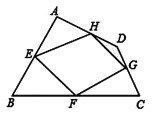
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,证明你的结论;
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形(不证明)
(3)你学过的哪种特殊四边形的中点四边形是矩形?_____(不证明)
【答案】 平行四边形 互相垂直 菱形
【解析】分析:(1)、连接BD,根据三角形中位线的性质得出EH∥FG,EH=FG,从而得出平行四边形;(2)、首先根据三角形中位线的性质得出平行四边形,根据对角线垂直得出一个角为直角,从而得出矩形;(3)、根据菱形的性质和三角形中位线的性质得出平行四边形,然后根据对角线垂直得出矩形.
详解:(1)证明:连结BD.
∵E、H分别是AB、AD中点, ∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD, ∴EH∥FG,EH=FG, ∴四边形EFGH是平行四边形
BD, ∴EH∥FG,EH=FG, ∴四边形EFGH是平行四边形
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.
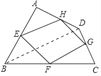
理由如下:如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点, ∴EH∥BD,HG∥AC,
∵AC⊥BD, ∴EH⊥HG, 又∵四边形EFGH是平行四边形, ∴平行四边形EFGH是矩形;
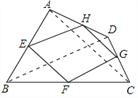
(3)菱形的中点四边形是矩形.理由如下:如图,连结AC、BD.
∵E、F、G、H分别为四边形ABCD四条边上的中点,∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD, ∴EH∥FG,EH=FG,
BD, ∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.∵四边形ABCD是菱形, ∴AC⊥BD,∵EH∥BD,HG∥AC,
∴EH⊥HG, ∴平行四边形EFGH是矩形.


科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=![]() ,b=
,b=![]() ,
,
求(2)中式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
,![]() 于R,
于R,![]() 于S,则四个结论正确的是
于S,则四个结论正确的是![]()
![]()
![]() 点P在
点P在![]() 的平分线上;
的平分线上;
![]() ;
;
![]() ;
;
![]() ≌
≌![]() .
.
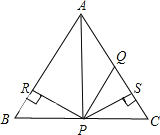
A. 全部正确 B. 仅![]() 和
和![]() 正确 C. 仅
正确 C. 仅![]() 正确 D. 仅
正确 D. 仅![]() 和
和![]() 正确
正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 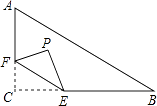
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表.

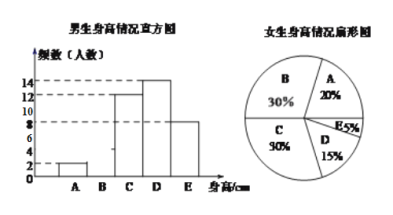
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)补充图中的男生身高情况直方图,男生身高的中位数落在_______组(填组别字母序号);
(2)在样本中,身高在150≤x<155之间的人数共有_______人,身高人数最多的在____组(填组别序号);
(3)已知该校共有男生400人,女生420人,请估计身高不足160的学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com