
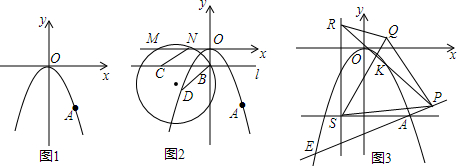
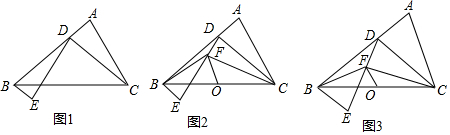
���� ��1���������ԭ��O����A��6��-6$\sqrt{3}$��������y��Ϊ�Գ����������Ϊy=ax2����A�������a���ɣ�
��2����ͼ2�У���CF��MN��F�����D��x��Ľ���Ϊ��x��0����D��m��-$\frac{\sqrt{3}}{6}$m2�������ݰ뾶����г����̣����M��N���꣬�Ƴ�MN=2$\sqrt{3}$����Rt��CFN�У���CN=2CF�Ƴ���FNC=30�㼴�ɽ�����⣮
��3����ͼ3�У��������֪ƽ��ֱ��CN������A��ֱ�ߵĽ���ʽΪy=$\frac{\sqrt{3}}{3}$x-8$\sqrt{3}$����ֱ��y=$\frac{\sqrt{3}}{3}$x-8$\sqrt{3}$��ֱ��x=-3�Ľ���ΪG����G��-3��-9$\sqrt{3}$�����ɡ�SQR�ա�PSH���Ƴ�SR=PG��RQ=SG���Ƴ�RQ=SG=3$\sqrt{3}$����DQ��n��D����n��x��Ľ���ΪM����RM=b����S��-3��-6$\sqrt{3}$�����Ƴ�MS=6$\sqrt{3}$���ɵ�P��6+$\frac{\sqrt{3}}{2}$b��$\frac{1}{2}$b-6$\sqrt{3}$���������PR�е�k���֤꣬��k��ֱ��y=$\sqrt{3}$-$\frac{9\sqrt{3}}{2}$���˶�����$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{6}{x}^{2}}\\{y=\sqrt{3}x-\frac{9}{2}\sqrt{3}}\end{array}\right.$��ȥy�õ�x2+6x-27=0��x=3��-9����������x=3������x=$\frac{3}{2}$+$\frac{\sqrt{3}}{4}$b�õ�b=2$\sqrt{3}$���ɴ˼��ɽ�����⣮
��� �⣺��1���������ԭ��O����A��6��-6$\sqrt{3}$��������y��Ϊ�Գ����������Ϊy=ax2��
��-6$\sqrt{3}$=36a��
��a=-$\frac{\sqrt{3}}{6}$��
��y=-$\frac{\sqrt{3}}{6}$x2��
��2����ͼ2�У���CF��MN��F�����D��x��Ľ���Ϊ��x��0����D��m��-$\frac{\sqrt{3}}{6}$m2����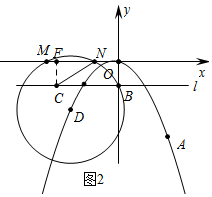
����x-m��2+��$\frac{\sqrt{3}}{6}$m2��2=m2+��-$\frac{\sqrt{3}}{6}$m2+$\sqrt{3}$��2��
������x2-2mx+m2-3=0��
��x=m+$\sqrt{3}$��m-$\sqrt{3}$��
��N��m+$\sqrt{3}$��0����M��m-$\sqrt{3}$��0��
��MN=2$\sqrt{3}$��
��Rt��CFN�У��ߡ�CFN=90�㣬CN=MN=2$\sqrt{3}$��CF=$\sqrt{3}$��
��CN=2CF��
���MNF=30�㣮
��3����ͼ3�У�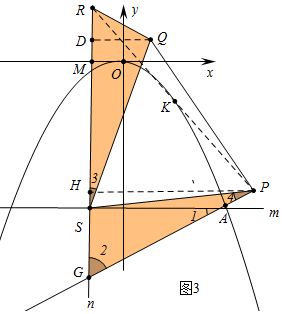
�������֪ƽ��ֱ��CN������A��ֱ�ߵĽ���ʽΪy=$\frac{\sqrt{3}}{3}$x-8$\sqrt{3}$��
��ֱ��y=$\frac{\sqrt{3}}{3}$x-8$\sqrt{3}$��ֱ��x=-3�Ľ���ΪG����G��-3��-9$\sqrt{3}$����
��m��x�ᣬ�ҹ���A��6��-6$\sqrt{3}$����
��S��-3��-6$\sqrt{3}$����
��SG=3$\sqrt{3}$��AS=9��
��tan��2=$\frac{AS}{SG}$=$\sqrt{3}$��
���2=60�㣬
���1=30�㣬
�ߡ�QRS=60��
���QRS=��2��
�ߡ�RSQ+��QSP=��2+��SPG����QSP=��2=60�㣬
���3=��4��
�ڡ�SQR�͡�PSG�У�
$\left\{\begin{array}{l}{��3=��4}\\{��QRS=��2}\\{SQ=SP}\end{array}\right.$��
���SQR�ա�PSH
��SR=PG��RQ=SG��
��RQ=SG=3$\sqrt{3}$����DQ��n��D��
��QRD=60�㣬
��DQ=$\sqrt{3}$DR=$\frac{\sqrt{3}}{2}$RQ=$\frac{9}{2}$��
��RD=$\frac{1}{2}$QR=$\frac{3\sqrt{3}}{2}$��
��n�ǹ���-3��0����y��ƽ�е�ֱ�ߣ���R��-3��b������n��x��Ľ���ΪM����RM=b��
��S��-3��-6$\sqrt{3}$����
��MS=6$\sqrt{3}$��
��SR=RM+MS=b+6$\sqrt{3}$=PG����PH��n��H��
�ߡ�2=60�㣬
��GH=$\frac{1}{2}$PG=$\frac{1}{2}$��b+6$\sqrt{3}$����
��MH=MG-HG=9$\sqrt{3}$-$\frac{1}{2}$��b+6$\sqrt{3}$��=6$\sqrt{3}$-$\frac{1}{2}$b��
��P��6+$\frac{\sqrt{3}}{2}$b��$\frac{1}{2}$b-6$\sqrt{3}$����
��K��PR�е㣬
��K��$\frac{3}{2}$+$\frac{\sqrt{3}}{4}$b��$\frac{3}{4}$b-3$\sqrt{3}$����
Ϊ�˷��㣬��K��x��y������x=$\frac{3}{2}$+$\frac{\sqrt{3}}{4}$b��y=$\frac{3}{4}$b-3$\sqrt{3}$����ȥb��y=$\sqrt{3}$x-$\frac{9}{2}$$\sqrt{3}$��
���е�K��ֱ��y=$\sqrt{3}$-$\frac{9\sqrt{3}}{2}$���˶���
��$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{6}{x}^{2}}\\{y=\sqrt{3}x-\frac{9}{2}\sqrt{3}}\end{array}\right.$��ȥy�õ�x2+6x-27=0��
��x=3��-9����������
��x=3������x=$\frac{3}{2}$+$\frac{\sqrt{3}}{4}$b�õ�b=2$\sqrt{3}$��
��RM=2$\sqrt{3}$��DM=RM-RD=2$\sqrt{3}$-$\frac{3}{2}$$\sqrt{3}$=$\frac{1}{2}$$\sqrt{3}$��
��$\frac{9}{2}$-3=$\frac{3}{2}$��
���Q��������$\frac{3}{2}$��$\frac{1}{2}$$\sqrt{3}$����
���� ���⿼����κ����ۺ��⡢����ϵ��������Ԫһ�η��̡������顢ȫ�������ε��ж������ʡ�����ǵ�ֱ�������ε����ʵ�֪ʶ���ڶ�������Ĺؼ������MN�ij�������������Ĺؼ��Ƿ���ȫ�������Σ�ѧ�����ò���������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
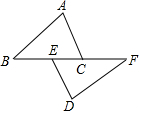 ��ͼ��AB=DF��AC=DE��BE=FC���ʣ���ABC���DEFȫ����AB��DFƽ������˵��������ɣ�
��ͼ��AB=DF��AC=DE��BE=FC���ʣ���ABC���DEFȫ����AB��DFƽ������˵��������ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2+3x | B�� | y=2+3x2 | C�� | y=$\frac{x}{2}$ | D�� | y=$\frac{1}{2x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2��y3 | B�� | y1��y3��y2 | C�� | y2��y3��y1 | D�� | y3��y1��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
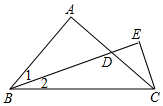 ��Rt��ABC�У���BAC=90�㣬AB=AC��CE��BD���ӳ�����E����1=��2����֤��BD=2CE��
��Rt��ABC�У���BAC=90�㣬AB=AC��CE��BD���ӳ�����E����1=��2����֤��BD=2CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
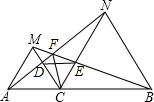 ��ͼ����CΪ�߶�AB��һ�㣬��ACM����CBN�ǵȱ������Σ�����֤����CFƽ�֡�AFB��
��ͼ����CΪ�߶�AB��һ�㣬��ACM����CBN�ǵȱ������Σ�����֤����CFƽ�֡�AFB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com