
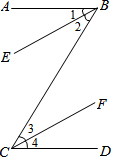
 补全下题的证明过程(括号里面填依据).
补全下题的证明过程(括号里面填依据).分析 利用角平分线定义得到∠EBC=$\frac{1}{2}$∠ABC,∠BCF=$\frac{1}{2}$∠BCD,由AB与CD平行,利用两直线平行内错角相等得到∠ABC=∠BCD,等量代换得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答 解:∵AB∥CD(已知)
∴∠ABC=∠BCD(两直线平行,内错角相等)
∵BE平分∠ABC (已知)
∴∠2=$\frac{1}{2}$∠ABC (角平分线的定义)
同理:∠3=$\frac{1}{2}$∠BCD,
∴∠2=∠3 (等量代换)
∴BE∥CF (内错角相等,两直线平行)
故答案为:BCD,两直线平行,内错角相等;角平分线的定义;BCD;等量代换;内错角相等,两直线平行.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
 一位旅行者在早晨8时从城市出发到乡村,第一个小时走了5千米,然后他上坡,1个小时只走了3千米,以后就休息;休息后平均每小时走4千米,在中午12时到达乡村.根据下图回答问题:
一位旅行者在早晨8时从城市出发到乡村,第一个小时走了5千米,然后他上坡,1个小时只走了3千米,以后就休息;休息后平均每小时走4千米,在中午12时到达乡村.根据下图回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
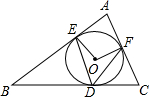 如图,⊙O内切于△ABC,切点分别为D、E、F,已知∠B=45°,∠C=65°,连接OE、OF、DE、DF,那么∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D、E、F,已知∠B=45°,∠C=65°,连接OE、OF、DE、DF,那么∠EDF等于( )| A. | 45° | B. | 50° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线a∥b,∠3=85°,求∠1、∠2的度数,根据下面的解答过程,填空或填写理由.
如图,直线a∥b,∠3=85°,求∠1、∠2的度数,根据下面的解答过程,填空或填写理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学了全等三角形的判定后,小明编了这样一个题目:“已知:如图,AB=AC,AD=AE,∠AEC=∠ADB,求证:△ABD≌△ACE.”老师说他的已知条件给多了,那么可以去掉的一个已知条件是:∠AEC=∠ADB.去掉上述条件后,请你完成证明.
学了全等三角形的判定后,小明编了这样一个题目:“已知:如图,AB=AC,AD=AE,∠AEC=∠ADB,求证:△ABD≌△ACE.”老师说他的已知条件给多了,那么可以去掉的一个已知条件是:∠AEC=∠ADB.去掉上述条件后,请你完成证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | B. | 旅客上飞机前的安检 | ||
| C. | 了解全市中小学生每天的零花钱 | D. | 学校招聘教师,对应聘人员面试 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com