
【题目】已知:在△ABC和△DCE中,∠ACB=∠DCE=90°,AC=DC,BC=EC,AB与DE相交于点F.
(1)如图1,求证AB=DE;
(2)如图2,连接CF,求证∠AFC=∠EFC;
(3)如图3,在(2)的条件下,当AF=EF时,连接BD,AE,延长CF交BD于点G,AE交CF于点H,若AE=8,BG=2,求线段GH的长.

【答案】(1)证明见解析;(2)证明见解析;(3)2.
【解析】
(1)证明△ABC≌△DEC(SAS),可得结论;
(2)如图2,作垂线段CM和CN,证明△ACM≌△DCN(AAS),得CM=CN,根据角平分线的逆定理可得:∠AFC=∠EFC;
(3)如图3,先证明△AFC≌△EFC,得AC=EC=BC,再证明△ACH≌△CBG(AAS),得CG和CH的长,利用线段的差可得结论.
证明:(1)如图1,在△ABC和△DEC中,
∵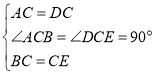 ,
,
∴△ABC≌△DEC(SAS),
∴AB=DE;
(2)如图2,过点C作CM⊥AB,CN⊥DE,垂足分别为M,N,
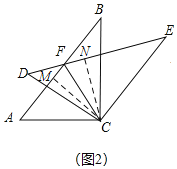
∵△ABC≌△DEC,
∴∠A=∠D,
在△ACM和△DCN中,
∵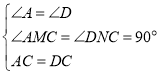 ,
,
∴△ACM≌△DCN(AAS),
∴CM=CN,
∴∠AFC=∠EFC;
(3)如图3,∵AB=DE,AF=EF,
∴AB-AF=DE-EF,即BF=DF,
∵∠AFC=∠EFC,∠AFC=∠BFG,∠EFC=∠DFG,
∴∠BFG=∠DFG,
∴FG⊥BD
∴∠BGF=∠DGF=90°,
同理∠AHF=∠EHF=90°,AH=EH=![]() AE=4,
AE=4,
在△AFC和△EFC中
∵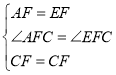
∴△AFC≌△EFC,
∴AC=EC,
∴AC=BC,
∵∠CBG+∠BCG=90°,∠ACH+∠BCG=90°,
∴∠CBG=∠ACH,
在△ACH和△CBG中,
∵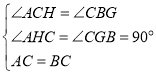 ,
,
∴△ACH≌△CBG(AAS),
∴CH=BG=2,CG=AH=4,
∴GH=CG-CH=4-2=2.


科目:初中数学 来源: 题型:
【题目】已知y1=a1(x﹣m)2+5,点(m,25)在抛物线y2=a2x2+b2x+c2上,其中m>0.
(1)若a1=﹣1,点(1,4)在抛物线y1=a1(x﹣m)2+5上,求m的值;
(2)记O为坐标原点,抛物线y2=a2x2+b2x+c2的顶点为M,若c2=0,点A(2,0)在此抛物线上,∠OMA=90°,求点M的坐标;
(3)若y1+y2=x2+16x+13,且4a2c2﹣b22=﹣8a2,求抛物线y2=a2x2+b2x+c2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.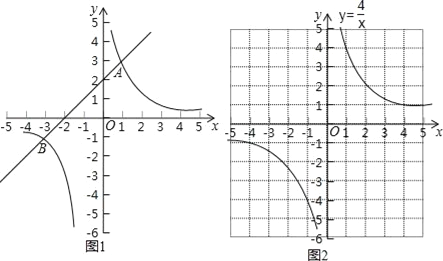
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“莲城读书月”活动结束后,对八年级(三)班45人所阅读书籍数量情况的统计结果如下表所示:
阅读数量 | 1本 | 2本 | 3本 | 3本以上 |
人数(人) | 10 | 18 | 13 | 4 |
根据统计结果,阅读2本书籍的人数最多,这个数据2是( )
A.平均数 B.中位数 C.众数 D.方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3,用<a>表示大于a的最小整数.例如:<2.5>=3,<4>=5,<-1.5>=-1.解决下列问题:
(1)[-2.6]=______,<6.2>=______.
(2)已知x,y满足方程组 ,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
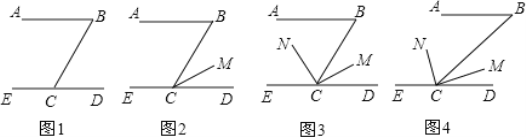
【题目】 (1)①如图1,已知AB∥CD,∠ABC=60°,可得∠BCD=_______°;
②如图2,在①的条件下,如果CM平分∠BCD,则∠BCM=_________°;
③如图3,在①、②的条件下,如果CN⊥CM,则∠BCN=___________°.
(2)、尝试解决下面问题:已知如图4,AB∥CD,∠B=40°,CN是∠BCE的平分线, CN⊥CM,求∠BCM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )

A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一批电子白板和一批笔记本电脑,经投标,购买1块电子白板比买3台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买1块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况,需购买电子白板和笔记本电脑的总数为396,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,连接AC.若AC=8,则四边形ABCD的面积为( )

A.32B.24C.40D.36
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com