
【题目】某校开展了以“人生观、价值观”为主题的班队活动.活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调査(要求每位同学只选自己最认可的一项观点),并制成了如图所示的扇形统计图. 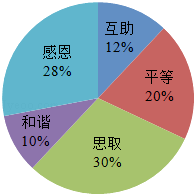
(1)该班学生选择“和谐”观点的有人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 .
(2)如果该校有1500名初三学生.利用样本估计选择“感恩”观点的初三学生约有人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查.求恰好选到“和谐”和“感恩”观点的概率.
【答案】
(1)5;36°
(2)420
(3)解:
互动 | 平等 | 思取 | 和谐 | 感恩 | |
互动 | (互动,平等) | (互动,思取) | (互动,和谐) | (互动,感恩) | |
平等 | (平等,互动) | (平等,思取) | (平等,和谐) | (平等,感恩) | |
思取 | (思取,互动) | (思取,平等) | (思取,和谐) | (思取,感恩) | |
和谐 | (和谐,互动) | (和谐,平等) | (和谐,思取) | (和谐,感恩) | |
感恩 | (感恩,互动) | (感恩,平等) | (感恩,思取) | (感恩,和谐) |
∴恰好选到“和谐”和“感恩”观点的概率= ![]()
【解析】解:(1)共调查了50名学生,选择“和谐”观点的占10%, 50×10%=5,360°×10%=36°;(2)∵选择“感恩”的占28%,
∴1500×28%=420人,
【考点精析】根据题目的已知条件,利用扇形统计图和列表法与树状图法的相关知识可以得到问题的答案,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.


科目:初中数学 来源: 题型:
【题目】某校将举办“心怀感恩孝敬父母”的活动,为此,校学生会就全校1 000名同学暑假期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成如下条形统计图. 
(1)本次调查抽取的人数为 , 估计全校同学在暑假期间平均每天做家务活的时间在40分钟以上(含40分钟)的人数为;
(2)校学生会拟在表现突出的甲、乙、丙、丁四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到甲、乙两名同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于![]() EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=![]() DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH=![]() S四边形ABCH.
S四边形ABCH.
其中正确的有( )

A. ①②③ B. ①③④ C. ②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
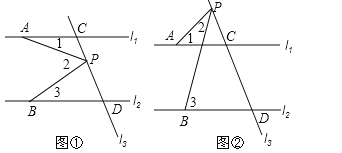
【题目】已知直线![]() ,直线
,直线![]() 与
与![]() 、
、![]() 分别交于C、D两点,点P是直线
分别交于C、D两点,点P是直线![]() 上的一动点.
上的一动点.
(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有![]() 这一相等关系?试说明理由;
这一相等关系?试说明理由;
(2)如图,当动点P在线段CD之外且在![]() 的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧 ![]() 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H. 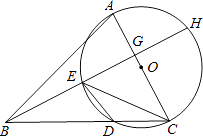
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com