
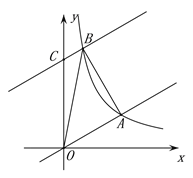
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
(1)求该反比例函数的关系式;
(2)将直线y=![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
【答案】(1) y=![]() (2)
(2) ![]() (3) P(7
(3) P(7![]() ,7)
,7)
【解析】(1)、首先根据一次函数的解析式求出点A的坐标,然后将点A代入反比例函数解析式得出k的值;(2)、首先得出平移后的解析式,然求出直线AB的解析式,得出AB和OA的长度,从而得出答案;(3)、根据△APB和△ABO相似得出AP和OP的长度,从而得出点P的坐标.
(1)、∵点A(m,3)在直线y=![]() x上, ∴3=
x上, ∴3=![]() m,m=
m,m=![]() ,∴点A(
,∴点A(![]() ,3)
,3)
∵点A(![]() ,3)在反比例函数y=
,3)在反比例函数y=![]() 上,∴k=
上,∴k=![]() ×3=
×3=![]() , ∴y=
, ∴y=![]() ;
;
(2)、直线向上平移8个单位后表达式为:y=![]() x +8
x +8
∵AB⊥OA,直线AB过点A(![]() ,3), ∴直线AB解析式:
,3), ∴直线AB解析式:![]() ,
,
∴![]() . ∴x=
. ∴x=![]() .∴B(
.∴B(![]() ,9) ,∴AB=4
,9) ,∴AB=4![]() ;
;
又∵OA=6,∴tan∠AOB=![]() ;
;
(3)、∵△APB∽△ABO ,∴![]() , 即
, 即![]() ,
,
∴AP=8, ∴OP=14, ∴P(7![]() ,7).
,7).


科目:初中数学 来源: 题型:
【题目】某校实验课程改革,初三年级设罝了A,B,C,D四门不同的拓展性课程(每位学生只选修其中一门,所有学生都有一门选修课程),学校摸底调査了初三学生的选课意向,并将调查结果绘制成两个不完整的统计图,问该校初三年级共有多少学生?其中要选修B、C课程的各有多少学生?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A为⊙C上一点,过点A作弦AB,取弦AB上一点P,若满足![]() ≤
≤![]() <1,则称P为点A关于⊙C的黄金点.已知⊙C的半径为3,点A的坐标为(1,0).
<1,则称P为点A关于⊙C的黄金点.已知⊙C的半径为3,点A的坐标为(1,0).
(1)当点C的坐标为(4,0)时,
①在点D(3,0),E(4,1),F(7,0)中,点A关于⊙C的黄金点是 ;
②直线![]() 上存在点A关于⊙C的黄金点P,求点P的横坐标的取值范围;
上存在点A关于⊙C的黄金点P,求点P的横坐标的取值范围;
(2)若y轴上存在点A关于⊙C的黄金点,直接写出点C横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,AB=CD=AD=5cm,BC=11cm,点P从点D开始沿DA边以每秒1cm的速度移动,点Q从点B开始沿BC边以每秒2cm的速度移动(当点P到达点A时,点P与点Q同时停止移动),假设点P移动的时间为x(秒),四边形ABQP的面积为y(cm2).
(1)求y关于x函数解析式,并写出它的定义域;
(2)在移动的过程中,PQ是否可能平分对角线AC?若能,求出x的值;若不能,请说明理由;
(3)在移动的过程中,是否从在x使得PQ=AB,若存在求出所有x的值,若不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=![]() ,则△EFC的周长为_____________.
,则△EFC的周长为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,(1)已知D是等腰△ABC底边BC上一点,DE∥AC,交AB于点E.DF∥AB,交AC于点F.请你探究DE、DF、AB之间的关系,并说明理由.(2)如图2所示,已知D是等腰△ABC底边BC延长线上一点,DE∥AC,交BA的延长线于点E.DF∥AB,交AC的延长线于点F.请你探究DE、DF、AB之间的关系,并说明理由.
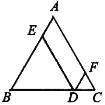
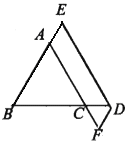
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
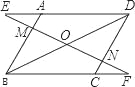
【题目】已知:如图在平行四边形ABCD中,过对角线BD的中点O作直线EF分别交DA的延长线、AB、DC、BC的延长线于点E、M、N、F.
(1)观察图形并找出一对全等三角形:△_≌△_,请加以证明;
(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)已知x﹣2的平方根是±4,2x﹣y+12的立方根是4,求![]() 的值;
的值;
(2)在Rt△ABC中,∠C=90°,若c=10cm,a:b=3:4,求△ABC的周长;
(3)已知a=![]() ,b=
,b=![]() ,试求a2+b2、a2+3ab+b2的值.
,试求a2+b2、a2+3ab+b2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com