
【题目】小峰和小轩用两枚质地均匀的骰子做游戏,规则如下:每人随机掷两枚骰子一次(若掷出的两枚骰子摞在一起,则重掷),点数和大的获胜;点数和相同为平局.
依据上述规则,解答下列问题:
(1)随机掷两枚骰子一次,用列表法或树状图法求点数和为10的概率;
(2)小峰先随机掷两枚骰子一次,点数和是10,求小轩随机掷两枚骰子一次,胜小峰的概率.(骰子:六个面分别有1、2、3、4、5、6个小圆点的立方块.点数和:两枚骰子朝上的点数之和.)
科目:初中数学 来源: 题型:
【题目】现有甲,乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克,甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同,两种机器人每小时分别搬运多少千克?设甲型机器人每小时搬运x千克,根据题意,可列方程为( )
A. ![]() =
=![]() B.
B. ![]() =
=![]()
C. ![]() =
=![]() D.
D. ![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx与x轴交于点A,顶点B的坐标为(﹣2,﹣2).
(1)求a,b的值;
(2)在y轴正半轴上取点C(0,4),在点A左侧抛物线上有一点P,连接PB交x轴于点D,连接CB交x轴于点F,当CB平分∠DCO时,求点P的坐标;
(3)在(2)的条件下,连接PC,在PB上有一点E,连接EC,若∠ECB=∠PDC,求点E的坐标.
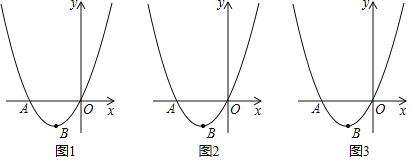
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点D的坐标为(﹣1,4),抛物线与x轴相交于A.B两点(A在B的左侧),与y轴交于点C(0,3).
(1)求抛物线的表达式;
(2)如图1,已知点E(0,﹣3),在抛物线的对称轴上是否存在一点F,使得△CEF的周长最小,如果存在,求出点F的坐标;如果不存在,请说明理由;
(3)如图2,连接AD,若点P是线段OC上的一动点,过点P作线段AD的垂线,在第二象限分别与抛物线、线段AD相交于点M、N,当MN最大时,求△POM的面积.
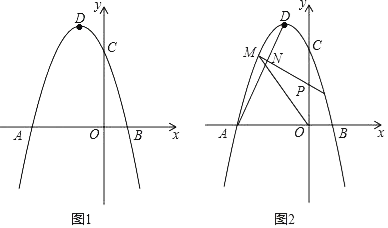
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() 、
、![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)若抛物线![]() 与抛物线
与抛物线![]() 关于
关于![]() 轴对称,在抛物线
轴对称,在抛物线![]() 位于第二象限的部分上取一点
位于第二象限的部分上取一点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
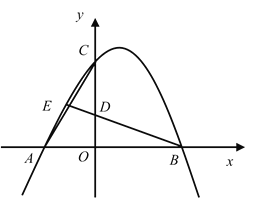
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD内接于⊙O,AB=AC,BD为⊙O的直径,AE⊥BD,垂足为点E,交BC于点F.
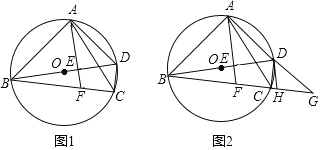
(1)求证:FA=FB;
(2)如图2,分别延长AD,BC交于点G,点H为FG的中点,连接DH,若tan∠ACB=![]() ,求证:DH为⊙O的切线;
,求证:DH为⊙O的切线;
(3)在(2)的条件下,若DA=3![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
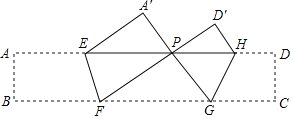
【题目】如图,把矩形ABCD沿EF,GH折叠,使点B,C落在AD上同一点P处,∠FPG=90°,△A′EP的面积是8![]() ,△D′PH的面积是4
,△D′PH的面积是4![]() ,则矩形ABCD的面积等于_____.
,则矩形ABCD的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
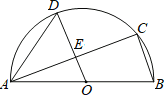
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=10,AC=8,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com