
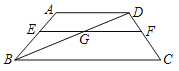
【题目】如图,在梯形ABCD中,点E,F分别在边AB,CD上,AD∥EF∥BC,EF与BD交于点G,AD=5,BC=10,![]() =
=![]() .
.
(1)求EF的长;
(2)设![]() =
=![]() ,
,![]() =
=![]() ,那么
,那么![]() = ,
= ,![]() = .(用向量
= .(用向量![]() 、
、![]() 表示)
表示)
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到![]() 这个等式,请解答下列问题:
这个等式,请解答下列问题:
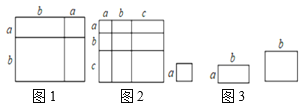
(1)写出图2中所表示的数学等式 .
(2)根据整式乘法的运算法则,通过计算验证上述等式.
(3)利用(1)中得到的结论,解决下面的问题:
若![]() ,
,![]() ,则
,则![]() .
.
(4)小明同学用图3中![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张长宽分别为
张长宽分别为![]() 、
、![]() 的长方形纸片拼出一个面积为
的长方形纸片拼出一个面积为![]() 的长方形,则
的长方形,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
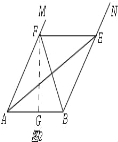
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
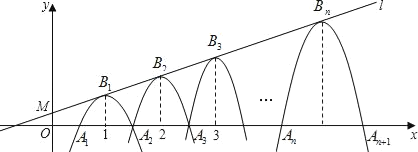
【题目】定义:若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线被称为:“直角抛物线”.如图,直线l:y=![]() x+b经过点M(0,
x+b经过点M(0,![]() ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn) (n为正整数),依次是直线l上的点,第一个抛物线与x轴正半轴的交点A1(x1,0)和A2(x2,0),第二个抛物线与x轴交点A2(x2,0)和A3(x3,0),以此类推,若x1=d(0<d<1),当d为_____时,这组抛物线中存在直角抛物线.
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn) (n为正整数),依次是直线l上的点,第一个抛物线与x轴正半轴的交点A1(x1,0)和A2(x2,0),第二个抛物线与x轴交点A2(x2,0)和A3(x3,0),以此类推,若x1=d(0<d<1),当d为_____时,这组抛物线中存在直角抛物线.
查看答案和解析>>
科目:初中数学 来源: 题型:
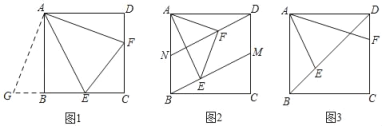
【题目】已知:正方形ABCD,∠EAF=45°.
(1)如图,当点E、F分别在边BC、CD上,连接EF,求证:EF=BE+DF;
童威同学是这样思考的,请你和他一起完成如下解答:证明:将△ADF绕点A顺时针旋转90°,得△ABG,所以△ADF≌△ABG.
(2)如图,点M、N分别在边AB、CD上,且BN=DM.当点E、F分别在BM、DN上,连接EF,探究三条线段EF、BE、DF之间满足的数量关系,并证明你的结论.
(3)如图,当点E、F分别在对角线BD、边CD上.若FC=2,则BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
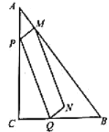
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、射线
、射线![]() 上,且
上,且![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,联结
,联结![]() ,以
,以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,设
,设![]() ,平行四边形
,平行四边形![]() 的面积为
的面积为![]() .
.
(1)当平行四边形![]() 为矩形时,求
为矩形时,求![]() 的正切值;
的正切值;
(2)当点![]() 在
在![]() 内,求
内,求![]() 关于
关于![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(3)当过点![]() 且平行于
且平行于![]() 的直线经过平行四边形
的直线经过平行四边形![]() 一边的中点时,直接写出
一边的中点时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD,并与棱BB'交于点Q.此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:
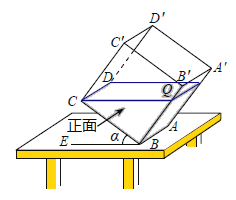
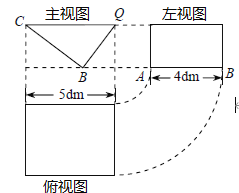
(1)CQ与BE的位置关系是 ,BQ的长是 dm:
(2)求液体的体积;(提示:直棱柱体积=底面积×高)
(3)若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°=![]() ,tan37°=
,tan37°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
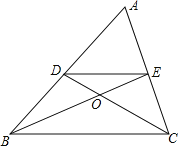
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE交CD于点O,连接DE,有下列结论:①DE=![]() BC;②△BOC∽△COE;③BO=2EO;④AO的延长线经过BC的中点.其中正确的是____.(填写所有正确结论的编号)
BC;②△BOC∽△COE;③BO=2EO;④AO的延长线经过BC的中点.其中正确的是____.(填写所有正确结论的编号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
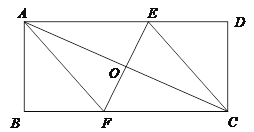
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com