
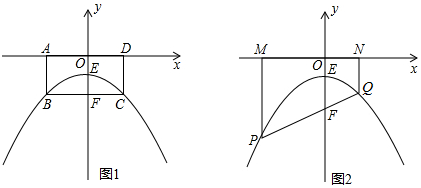
分析 (1)由题意得出抛物线顶点E(0,-1),再设顶点式根据点B坐标可得抛物线解析式;
(2)①设点P(x,-$\frac{1}{4}$x2-1),知PM=|-$\frac{1}{4}$x2-1|=$\frac{1}{4}$x2+1,根据两点间的距离公式求得PF=$\sqrt{(0-x)^{2}+(-2+\frac{1}{4}{x}^{2}+1)^{2}}$=$\frac{1}{4}$x2+1,即可得PM=PF,同理可得QN=QF,从而得证;
②由PM+PN=PQ=m,结合S四边形PMNQ=$\frac{\sqrt{3}}{4}$m2,即$\frac{1}{2}$(PM+PN)×MN=$\frac{\sqrt{3}}{4}$m2知MN=$\frac{\sqrt{3}}{2}$m,继而利用勾股定理得出QH的长,即可得直线PQ的斜率k,由直线过点F(0,-2)可得答案.
解答 解:(1)由题意知点E(0,-1),
设抛物线解析式为y=ax2-1,
将点B(-2,-2)代入,得:-2=4a-1,
解得:a=-$\frac{1}{4}$,
∴y=-$\frac{1}{4}$x2-1,
则a=-$\frac{1}{4}$,b=0,c=-1,
故答案为:-$\frac{1}{4}$,0,-1;
(2)①设点P(x,-$\frac{1}{4}$x2-1),则PM=|-$\frac{1}{4}$x2-1|=$\frac{1}{4}$x2+1,
∵点F(0,-2),
∴PF=$\sqrt{(0-x)^{2}+(-2+\frac{1}{4}{x}^{2}+1)^{2}}$
=$\sqrt{{x}^{2}+\frac{1}{16}{x}^{4}-\frac{1}{2}{x}^{2}+1}$
=$\sqrt{\frac{1}{16}{x}^{4}+\frac{1}{2}{x}^{2}+1}$
=$\sqrt{(\frac{1}{4}{x}^{2}+1)^{2}}$
=$\frac{1}{4}$x2+1,
∴PM=PF,
同理可得QN=QF,
则PM+QN=PF+QF=PQ;
②由①知,PM+PN=PQ=m,
∵S四边形PMNQ=$\frac{\sqrt{3}}{4}$m2,即$\frac{1}{2}$(PM+PN)×MN=$\frac{\sqrt{3}}{4}$m2,
∴MN=$\frac{\sqrt{3}}{2}$m,
如图,过点P作PH⊥NQ的延长线于点H,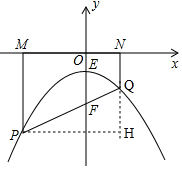
则PH=MN=$\frac{\sqrt{3}}{2}$m,
∴QH=$\sqrt{P{Q}^{2}-P{H}^{2}}$=$\sqrt{{m}^{2}-(\frac{\sqrt{3}}{2}m)^{2}}$=$\frac{m}{2}$,
∴kPQ=$\frac{QH}{PH}$=$\frac{\frac{m}{2}}{\frac{\sqrt{3}}{2}m}$=$\frac{\sqrt{3}}{3}$,
当点P在y轴右侧的抛物线上时,同理可得kPQ=-$\frac{\sqrt{3}}{3}$,
又∵PQ过点F(0,-2),
∴直线PQ对应的一次函数的解析式为y-(-2)=±$\frac{\sqrt{3}}{3}$(x-0),即y=±$\frac{\sqrt{3}}{3}$x-2.
点评 本题主要考查二次函数的综合,熟练掌握矩形的性质、待定系数法求二次函数解析式及勾股定理、两点间的距离公式、直线的解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
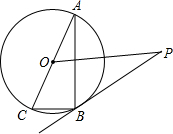 已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.
已知:如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com