
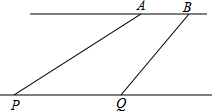
 码头A、B位于东西走向的河岸线l上,一游轮在P处测得码头A在其北偏东70°,游轮向东航行10分钟后到达Q处,此时测得码头B在其北偏东35°.已知游轮的速度为30千米/小时,两码头A、B相距2千米.
码头A、B位于东西走向的河岸线l上,一游轮在P处测得码头A在其北偏东70°,游轮向东航行10分钟后到达Q处,此时测得码头B在其北偏东35°.已知游轮的速度为30千米/小时,两码头A、B相距2千米.| 3 |
| 5 |
| 4 |
| 5 |
| 7 |
| 10 |
| 9 |
| 10 |
| 7 |
| 20 |
| 27 |
| 10 |
| 7 |
| 4 |
| 7 |
| 4 |
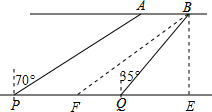 解:(1)过点B作BE⊥PQ于E,作BF∥AP交PQ于点F.
解:(1)过点B作BE⊥PQ于E,作BF∥AP交PQ于点F.| 10 |
| 60 |
| BQ |
| sin∠BFQ |
| FQ |
| sin∠FBQ |
| BQ | ||
|
| 3 | ||
|
| 7 |
| 4 |
| 7 |
| 4 |
| 4 |
| 5 |
| 7 |
| 5 |
| 7 |
| 5 |
| 7 |
| 4 |
| 7 |
| 4 |
| 7 |
| 120 |
| 7 |
| 120 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| A、0.398×106亿元 |
| B、3.98×105亿元 |
| C、39.8×104亿元 |
| D、398×103亿元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com