
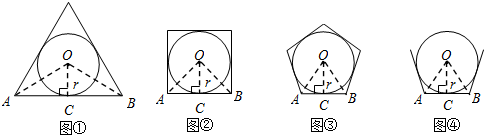
分析 (1)设AB切⊙P于点C,连接OC,OA,OB,求出∠AOC,在RT△AOC中求出AC,求出△AOB的面积即可解决问题.
(2)类似(1).
(3)类似(1).
解答 解:(1)如图②中,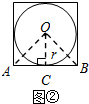
设AB切⊙P于点C,连接OC,OA,OB
∴OC⊥AB,
∴OA=OB,
∴∠AOC=$\frac{1}{2}$∠AOB,∴AB=2BC.
在Rt△AOC中,
∵∠AOC=$\frac{1}{2}$•$\frac{360°}{4}$=45°,OC=r,
∴AC=r•tan45°,∴AB=2r•tan45°,
∴S△OAB=$\frac{1}{2}$•r•2r•tan60°=r2tan45°,
∴S正四边形=4S△OAB=4r2•tan45°.
故答案为4r2•tan45°
(2)如图③中,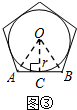
设AB切⊙P于点C,连接OC,OA,OB,
∴OC⊥AB,
∴OA=OB,
∴∠AOC=$\frac{1}{2}$∠AOB,∴AB=2BC.
在Rt△AOC中,
∵∠AOC=$\frac{1}{2}$•$\frac{360°}{5}$=36°,OC=r,
∴AC=r•tan36°,∴AB=2r•tan36°,
∴S△OAB=$\frac{1}{2}$•r•2r•tan36°=r2tan36°,
∴S正五边形=5S△OAB=5r2•tan36°.
(3)如图④中,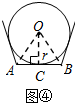
设AB切⊙P于点C,连接OC,OA,OB,
∴OC⊥AB,
∴OA=OB,
∴∠AOC=$\frac{1}{2}$∠AOB,∴AB=2BC.
在Rt△AOC中,
∵∠AOC=$\frac{1}{2}$•$\frac{360°}{n}$=$\frac{180°}{n}$,OC=r,
∴AC=r•tan$\frac{180°}{n}$,
∴AB=2r•tan$\frac{180°}{n}$,
∴S△OAB=$\frac{1}{2}$•r•2r•tan$\frac{180°}{n}$=r2tan$\frac{180°}{n}$,
∴S正n边形=n•S△OAB=n•r2•tan$\frac{180°}{n}$.
故答案为n•r2•tan$\frac{180°}{n}$.
点评 本题考查圆的综合题、锐角三角函数、等腰三角形的性质、正多边形的面积等知识,解题的关键是把多边形转化为三角形,记住多边形的中心角=$\frac{360°}{n}$,学会灵活应用锐角三角函数,属于中考常考题型.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
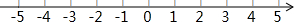 解不等式组$\left\{\begin{array}{l}{\frac{x}{2}>-1①}\\{2x+1≥5(x-1)②}\end{array}\right.$,并把它的解集在如图所示顶点数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{\frac{x}{2}>-1①}\\{2x+1≥5(x-1)②}\end{array}\right.$,并把它的解集在如图所示顶点数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一步 | B. | 第二步 | C. | 第三步 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-b<0 | B. | $\frac{a}{3}$<$\frac{b}{3}$ | C. | 1-a<1-b | D. | -1+a<-1+b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4+3x=25 | B. | 3×4-3x=25 | C. | 3×4+3x=25 | D. | 3(4-x)=25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com