
 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CN}$的值为( )
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则$\frac{OC}{CN}$的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
 四张形状相同的卡片如图所示.将卡片洗匀后背面朝上放置在桌面上,小明先随机抽一张卡片,记下数字为x;小亮再随机抽一张卡片,记下数字为y.两人在此基础上共同协商一个游戏规则:当x>y时小明获胜,否则小亮获胜
四张形状相同的卡片如图所示.将卡片洗匀后背面朝上放置在桌面上,小明先随机抽一张卡片,记下数字为x;小亮再随机抽一张卡片,记下数字为y.两人在此基础上共同协商一个游戏规则:当x>y时小明获胜,否则小亮获胜查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a<\frac{1}{2}$ | B. | $a>\frac{1}{2}$ | C. | $a≥\frac{1}{2}$ | D. | $a≤\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
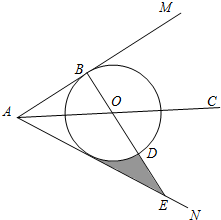 如图,AC平分∠MAN,点O在射线AC上,以点O为圆心,半径为1的⊙O与AM相切于点B,连接BO并延长交⊙O于点D,交AN于点E.
如图,AC平分∠MAN,点O在射线AC上,以点O为圆心,半径为1的⊙O与AM相切于点B,连接BO并延长交⊙O于点D,交AN于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一条宽相等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?
如图所示,有一条宽相等的小路穿过长方形的草地ABCD,若AB=60m,BC=84m,AE=100m,若要硬化这条小路,且每平方米造价50元,则需要多少元钱?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
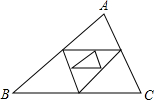 如图,已知△ABC的周长为1,连接△ABC的三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )
如图,已知△ABC的周长为1,连接△ABC的三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2015个三角形的周长为( )| A. | $\frac{1}{2014}$ | B. | $\frac{1}{2015}$ | C. | ($\frac{1}{2}$)2014 | D. | ($\frac{1}{2}$)2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com