
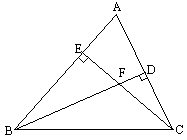
已知:在△ 中,
中,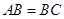 ,
,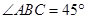 ,
, 于
于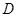 ,
,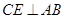 于点
于点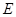 ,
, 、
、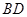 相交于
相交于 .
.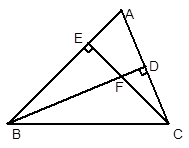
(1)求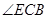 的度数;
的度数;
(2)求证:△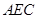 ≌△
≌△ ;
;
(3)探究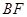 与
与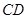 的数量关系,并给予证明.
的数量关系,并给予证明.
(1)45°;
(2)∵在△EBC中,∠ECB=∠ABC
∴EB=EC
∵在△ABC中,BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠BDC= 90°
∴∠A+∠ACE=∠A+∠ABD=90°
∴∠ACE=∠ABD
在△BEF与△CEA中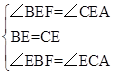
∴△BEF≌△CEA;
(3)BF=2CD
解析试题分析:(1)由CE⊥AB于E,∠ABC=45°,根据三角形的内角和为180°即可求得结果;
(2)先根据等角对等边可得EB=EC,再根据同角的余角相等可得∠ACE=∠ABD,再有CE⊥AB即得结论;
(3)由AB=CB,BD⊥AC于D,根据等腰三角形的三线合一的性质可得AC="2CD" ,再结合△BEF≌△CEA根据全等三角形的性质即可得到结果.
(1)∵在△ABC中,CE⊥AB于E
∴∠AEC=90°
又∵∠AEC=∠ABC+∠ECB,∠ABC=45°
∴∠ECB=∠AEC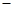 ∠ABC= 90°
∠ABC= 90°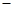 45°= 45°;
45°= 45°;
(2)∵在△EBC中,∠ECB=∠ABC
∴EB=EC
∵在△ABC中,BD⊥AC于D,CE⊥AB于E
∴∠BEC=∠BDC= 90°
∴∠A+∠ACE=∠A+∠ABD=90°
∴∠ACE=∠ABD
在△BEF与△CEA中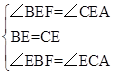
∴△BEF≌△CEA;
(3)∵在△ABC中,AB=CB,BD⊥AC于D,
∴AC="2CD"
∵△BEF≌△CEA
∴BF="AC"
∴BF=2CD.
考点:本题考查的是全等三角形的判定和性质
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


科目:初中数学 来源:黄冈难点课课练八年级数学下册(北师大版) 题型:044
如图所示,已知:在△ABC中,BD⊥AC于D,CE⊥AB于E,BD与CE交于点F.若∠A=![]() ,求∠BFC的度数.
,求∠BFC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com