
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交AE于点O,且点O在四边形ABCD的内部. 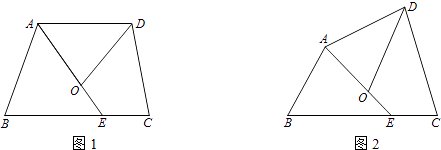
(1)如图1,若AD∥BC,∠B=70°,∠C=80°,则∠DOE=°.
(2)如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来
【答案】
(1)105
(2)解:∵∠DOE=∠OAD+∠ADO,
∵∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交AE于点O,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°
【解析】解:(1)∵AD∥BC,∠B=70°,∠C=80°, ∴∠BAD=110°,∠ADC=100°,
∵∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交AE于点O,
∴∠BAE=55°,∠ODC=50°,
∴∠AEC=125°,
∴∠DOE=360°﹣125°﹣80°﹣50°=105°;
所以答案是:105.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握多边形内角与外角(多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图1可以解释完全平方公式(a+b)2=a2+2ab+b2 . 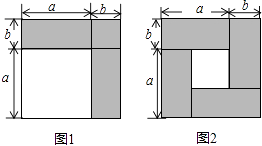
(1)如图2,请用不同的代数式表示图中阴影部分的面积,由此,你能得到怎样的等式?
(2)请说明这个等式成立;
(3)已知(2m+n)2=13,(2m﹣n)2=5,请利用上述等式求mn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com