
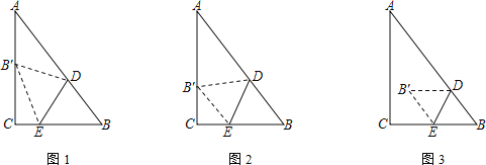
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D、E分别是AB和BC上的点.把△ABC沿着直线DE折叠,顶点B对应点是点B′
(1)如图1,点B′恰好落在线段AC的中点处,求CE的长;
(2)如图2,点B′落在线段AC上,当BD=BE时,求B′C的长;
(3)如图3,E是BC的中点,直接写出AB′的最小值.
【答案】(1)![]() ;(2)3;(3)
;(2)3;(3)![]()
【解析】
(1)设CE=x,则BE=6-x;在Rt△B'CE中,根据勾股定理列出关于x的方程,解方程即可解决问题.
(2)如图2中,作B′H⊥AB于H.连接BB′.首先证明B′C=B′H,设B′C=B′H=x,构建方程即可解决问题.
(3)如图3中,连接AE,EB′,AB′.在△AB′E中,利用三角形长三边关系即可解决问题.
解:(1)如图1中,
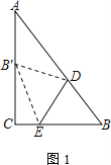
∵点B′落在AC的中点,
∴CB′=![]() AC=4,
AC=4,
设CE=x,则BE=6-x,
由折叠得:B'E=BE=8-x,
在Rt△B'CE中,由勾股定理得x2+42=(6-x)2
解得:x=![]() ,
,
即CE的长为![]() .
.
(2)如图2中,作B′H⊥AB于H.连接BB′.
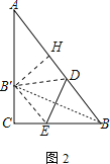
∵EB=EB′,DB=DB′,BE=BD,
∴BE=EB′=B′D=DB,
∴四边形BEB′D是菱形,
∴∠B′BD=∠B′BE,
∵B′C⊥BC,B′H⊥AB,
∴B′C=B′H,设B′C=B′H=x.
在Rt△ABC中,∵BC=6,AC=8,
∴AB=![]() =10,
=10,
∵S△ABC=S△BCB′+S△ABB′,
∴![]() ACBC=
ACBC=![]() BCx+
BCx+![]() ×AB×x,
×AB×x,
∴x=3,
∴CB′=3.
(3)如图3中,连接AE,EB′,AB′.
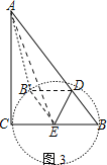
在Rt△ACE中,∵AC=8,EC=3,
∴AE=![]() =
=![]() ,
,
∵EB=EC=EB′=3,
∴AB′≥AE-BE′,
∴AB′≥![]() -3,
-3,
∴AB′的最小值为![]() -3.
-3.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
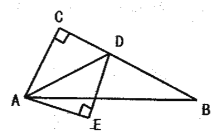
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰直角三角形
的下方作等腰直角三角形![]() .
.
(1)填空:![]() 的面积等于 ;
的面积等于 ;
(2)连接![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)点![]() 在
在![]() 边上,且
边上,且![]() , 当
, 当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,求点
停止时,求点![]() 相应的运动路程.
相应的运动路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
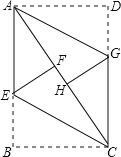
【题目】如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的两点,E、G分别是折痕CE、AG与AB、CD的交点.
(1)求证:四边形AECG是平行四边形:
(2)若AB=8cm,BC=6cm,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=(x-a)(x-3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP⊥x轴,垂足为点P,连接AD、BC.
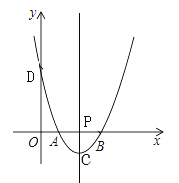
(1)求点A、B、D的坐标;
(2)若△AOD与△BPC相似,求a的值;
(3)点D、O、C、B能否在同一个圆上,若能,求出a的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
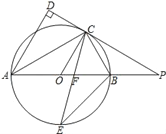
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:PC=PF;
(3)若tan∠ABC=![]() ,AB=14,求线段PC的长.
,AB=14,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O.
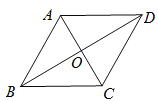
(1)尺规作图:以OA、OD为边,作矩形OAED(不要求写作法,但保留作图痕迹);
(2)若在菱形ABCD中,∠BAD=120 °,AD=2,求所作矩形OAED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年浙江义乌10分)小明合作学习小组在探究旋转、平移变换.如图△ABC,△DEF均为等腰直角三角形,各顶点坐标分别为A(1,1),B(2,2),C(2,1),D(![]() ,0),E(
,0),E(![]() , 0),F(
, 0),F(![]() ,
,![]() ).
).
(1)他们将△ABC绕C点按顺时针方向旋转450得到△A1B1C.请你写出点A1,B1的坐标,并判断A1C和DF的位置关系;
(2)他们将△ABC绕原点按顺时针方向旋转450,发现旋转后的三角形恰好有两个顶点落在抛物线![]() 上.请你求出符合条件的抛物线解析式;
上.请你求出符合条件的抛物线解析式;
(3)他们继续探究,发现将△ABC绕某个点旋转45,若旋转后的三角形恰好有两个顶点落在抛物线![]() 上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.
上,则可求出旋转后三角形的直角顶点P的坐标.请你直接写出点P的所有坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com