
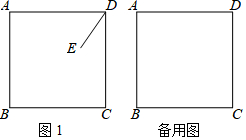
分析 (1)①根据题意补全图形,
②先判断出∠GDA=∠EDC,进而得出△AGD≌△CED,即可得出AG=CE,最后判断出∠AFH=∠HDC=90°即可得出结论;
(2)分两种情况,①当点G在线段BD的延长线上时和②当点G在线段BD上时,构造直角三角形利用勾股定理即可得出结论.
解答 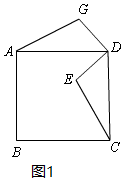
解:(1)当点E在正方形ABCD内部时,
①根依题意,补全图形如图1:
②AG=CE,AG⊥CE.
理由:
在正方形ABCD,
∴AD=CD,∠ADC=90°,
∵由DE绕着点D顺时针旋转90°得DG,
∴∠GDE=∠ADC=90°,GD=DE,
∴∠GDA=∠EDC
在△AGD和△CED中,$\left\{\begin{array}{l}{AD=CD}\\{∠GDA=∠EDC}\\{DG=DE}\end{array}\right.$,
∴△AGD≌△CED,
∴AG=CE.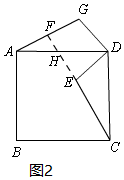
延长CE分别交AG、AD于点F、H,
由①中结论△AGD≌△CED,
∴∠GAD=∠ECD,
∵∠AHF=∠CHD,
∴∠AFH=∠HDC=90°,
∴AG⊥CE.
(2)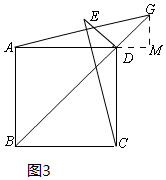
解:①当点G在线段BD的延长线上时,如图3所示.
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°.
∵GM⊥AD,DG=2$\sqrt{2}$
∴MD=MG=2,
∴AM=AD+DM=6
在Rt△AMG中,由勾股定理,得
AG=$\sqrt{A{M}^{2}+M{G}^{2}}$=2$\sqrt{10}$,
∴CE=AG=2$\sqrt{10}$
②当点G在线段BD上时,如图4所示,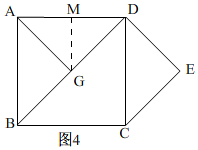
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADG=45°
∵GM⊥AD,DG=2$\sqrt{2}$
∴MD=MG=2,
∴AM=AD-MG=2
在Rt△AMG中,由勾股定理,得
AG=$\sqrt{A{M}^{2}+M{G}^{2}}$=2$\sqrt{2}$
∴CE=AG=2$\sqrt{2}$
故CE的长为2$\sqrt{2}$或2$\sqrt{10}$.
点评 此题是四边形综合题,主要考查了正方形的性质,全等三角形的判定和性质,勾股定理,解(1)的关键是判断出△AGD≌△CED,解(2)的关键是构造直角三角形,是一道中考常考题.


科目:初中数学 来源: 题型:选择题
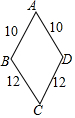 如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )
如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框,为保证稳定要在BD间加一根木条.设该木条的长为xcm,则x的取值范围是( )| A. | 0<x<20 | B. | 2<x<20 | C. | 0<x<24 | D. | 2<x<24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
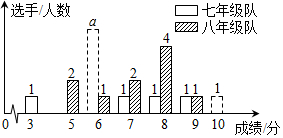
| 队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
| 八年级 | 7.1 | p | q | 1.69 | 80% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com