
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=3,D为BC边的中点,∠MDN=90°,将∠MDN绕点D顺时针旋转,它的两边分别交AB、AC于点E、F.

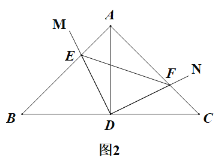
(1)求证:△ADE ≌ △CDF;
(2)求四边形AEDF的面积;
(3)如图2,连接EF,设BE=x,求△DEF的面积S与x之间的函数关系式.
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
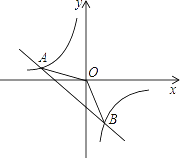
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边三角形AB1C1,再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边三角形AB2C2,再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形,得到第三个等边AB3C3;…,如此下去,这样得到的第n个等边三角形ABnCn的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合.若长方形的长BC为8,宽AB为4,求:
(1)CF的长;
(2)求三角形GED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为一个计算程序;

(1)若输入的x=3,则输出的结果为 ;
(2)若开始输入的x为正整数,最后输出的结果为40,则满足条件的x的不同值最多有 ;
(3)规定:程序运行到“判断结果是否大于30”为一次运算.若运算进行了三次才输出,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)如图①,在菱形ABCD中,∠ABC=120°,点M,N分别在AD,CD上,且∠MBN=60°,试判断四边形DMBN是否为“等邻边四边形”?请说明理由.
(2)如图②,在矩形ABCD中,AB=8,BC=12.5,点E在BC上,且BE=6,在矩形ABCD内或边上,确定一点P,使四边形ABEP为最大面积的“等邻边四边形”,若能实现,请求出最大面积;若不能实现,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
①金卡售价600元/张,每次凭卡不再收费.
②银卡售价150元/张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.

(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
(3)请根据函数图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4,2)、B(0,4)、C(0,2),

(1)画出△ABC关于点C成中心对称的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com