
分析 (1)根据乘法分配律计算即可.
(2)首先计算乘方和乘法,然后从左向右依次计算即可.
(3)根据除法的性质计算即可.
(4)首先计算乘方和括号里面的运算,然后计算减法即可.
解答 解:(1)(23$\frac{2}{3}$-29$\frac{7}{15}$+26.6-19$\frac{5}{9}$)×(-45)
=23$\frac{2}{3}$×(-45)-29$\frac{7}{15}$×(-45)+26.6×(-45)-19$\frac{5}{9}$×(-45)
=-1065+1326-1197+880
=-56
(2)-32+(-2$\frac{1}{2}$)2×(-$\frac{4}{25}$)+|-22|
=-9-1+4
=-6
(3)47$\frac{24}{25}$÷(-48)
=(48-$\frac{1}{25}$)÷(-48)
=48÷(-48)-$\frac{1}{25}$÷(-48)
=-1+$\frac{1}{1200}$
=-$\frac{1199}{1200}$
(4)-52-[-4+(1-0.2×$\frac{1}{5}$)÷(-2)]
=-25-[-4+$\frac{24}{25}$÷(-2)]
=-25-[-4-$\frac{12}{25}$]
=-25+4+$\frac{12}{25}$
=-20$\frac{13}{25}$
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算,注意乘法运算定律和除法的性质的应用.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
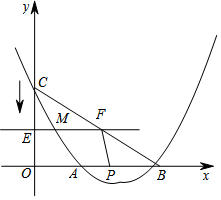 如图,抛物线y=a2+bx+c(a>0)交x轴于A(4,0)、B(8,0)两点,交y轴于点C,且$\frac{OC}{OB}$=$\frac{1}{2}$.
如图,抛物线y=a2+bx+c(a>0)交x轴于A(4,0)、B(8,0)两点,交y轴于点C,且$\frac{OC}{OB}$=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
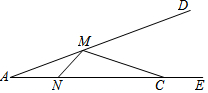 如图,已知∠DAE=22.5°,点C是射线AE上一点,且线段AC=3,若点M和点N分别是射线AD和线段AC上的两个动点,则MN+MC的最小值是$\frac{3\sqrt{2}}{2}$.
如图,已知∠DAE=22.5°,点C是射线AE上一点,且线段AC=3,若点M和点N分别是射线AD和线段AC上的两个动点,则MN+MC的最小值是$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
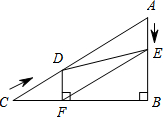 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com