
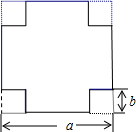
 如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米?
如图,在一块边长为a cm的正方形铁皮的四角各剪去一个边长为b cm的正方形(b<$\frac{a}{2}$),再把周围四个长方形沿虚线折起,制作成一个无盖的长方体盒子.当a=150cm,b=25cm,制作这样的一个长方体盒子至少需要铁皮多少平方厘米? 分析 在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<$\frac{a}{2}$)厘米的正方形,那么剩余部分的面积=a2-4b2,利用平方差公式分解因式,然后代入数值计算即可求解.
解答 解:依题意得大正方形纸板的面积是a2,四个小正方形的面积为4b2,则剩余部分的面积为a2-4b2;
∵a2-4b2=(a+2b)(a-2b),
∴当a=150,b=25时,剩余部分的面积=(150+50)(150-50)=20000(平方厘米).
故制作一个这样的无盖长方体盒子至少需要铁皮20000平方厘米
点评 此题主要考查了因式分解的应用,解题的关键是利用正方形的面积公式和熟练进行因式分解.


科目:初中数学 来源: 题型:选择题
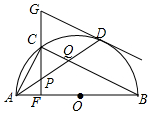 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CF⊥AB于点E,过点D的切线交FC的延长线于点G,连接AD,分别交CF、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是( )
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,弦CF⊥AB于点E,过点D的切线交FC的延长线于点G,连接AD,分别交CF、CB于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点P是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是( )| A. | ①②④ | B. | ②③⑤ | C. | ③④ | D. | ②⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
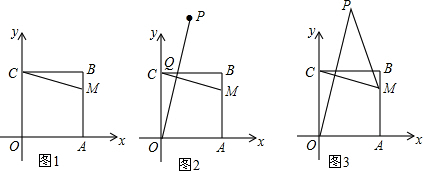
 如图,点A(3,2)和点M(m,n)都在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,点A(3,2)和点M(m,n)都在反比例函数y=$\frac{k}{x}$(x>0)的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品牌 | 每只销售利润/元 | 每周销售量/只 |
| A | x | -300x+1200 |
| B | 2 | 当0<x<3时,120x+140 当3≤x≤4时,500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com