
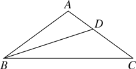
【题目】如图,在△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于点D.
(1)填空:∠DBC=_________度;
(2)猜想:BC、AB、CD三者数量关系_____________________;
(3)证明你的猜想.
【答案】(1)18;(2)BC=AB+CD;(3)证明详见解析
【解析】
(1)根据等腰三角形的性质及三角形的内角和得出∠ABC的度数,再根据角平分线的定义可得出结果;
(2)通过观察可初步猜想BC=AB+CD;
(3)在线段BC上截取BE=BA,连接DE.先证明△ABD≌△EBD,再结合角度证明∠CDE=∠CED,从而有CD=CE,最后通过等量代换即可得出结果.
解:(1)∵AB=AC,∠A=108°,
∴∠ACB=∠ABC=![]() ×(180°-108°)=36°,
×(180°-108°)=36°,
又BD平分∠ABC,
∴∠DBC=∠ABD=18°.
故答案为:18;
(2)BC=AB+CD.证明见(3),
故答案为:BC=AB+CD;
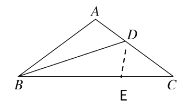
(3)证明:在线段BC上截取BE=BA,连接DE.
∵BD平分∠ABC,
∴∠ABD=∠EBD,
在△ABD和△EBD中,
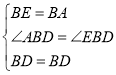 ,
,
∴△ABD≌△EBD(SAS),
∴∠BED=∠A=108°,∴∠DEC=72°,
又∵∠C=36°,
∴∠CED=∠CDE=72°,∴CD=CE,
∴BC=BE+EC=AB+CD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
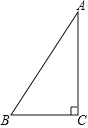
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司10名销售员,去年完成的销售额情况如表:
销售额(单位:万元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
销售员人数(单位:人) | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,AB、BC边上的垂直平分线相交于点P.若∠BAC=50°,则∠BPC的度数为( )
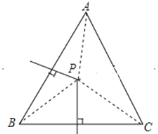
A.100°B.110°C.115°D.120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一定点,且
边上一定点,且![]() ,点
,点![]() 是线段
是线段![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() .当点
.当点![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,点
停止时,点![]() 的运动的路径长为_________.
的运动的路径长为_________.
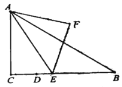
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.
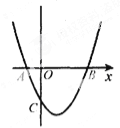
(1)点A的坐标为 点B的坐标为 ,点C的坐标为 ;
(2)设抛物线y=x2-2x-3的顶点坐标为M,求四边形ABMC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
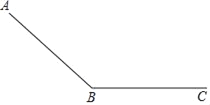
【题目】如图,一个滑道由滑坡(AB段)和缓冲带(BC段)组成,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s.
(1)求y1和t1满足的二次函数解析式;
(2)求滑坡AB的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com