
【题目】如图①,△ABC是等边三角形,点P是BC上一动点(点P与点B、C不重合),过点P作PM∥AC交AB于M,PN∥AB交AC于N,连接BN、CM.

(1)求证:PM+PN=BC;
(2)在点P的位置变化过程中,BN=CM是否成立?试证明你的结论;
(3)如图②,作ND∥BC交AB于D,则图②成轴对称图形,类似地,请你在图③中添加一条或几条线段,使图③成轴对称图形(画出一种情形即可).
【答案】(1)见解析;(2)结论成立,理由见解析;(3)见解析
【解析】
(1)先证明△BMP,△CNP是等边三角形,再证明△BPN≌△MPC,从而PM=PB,PN=PC,可得PM+PN=BC;
(2)BN=CM总成立,由(1)知△BPN≌△MPC,根据全等三角形的性质可得结论;
(3)作ND∥BC交AB于N,作ME∥BC交AC于M,作EF∥AB交BC于F,连接DF即可.
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∵PM∥AC,PN∥AB,
∴∠BPM=∠ACB=60°,∠CPN=∠ABC=60°,
∴△BMP,△CNP是等边三角形,
∴∠BPM=∠CPN=60°,PN=PC,PN=PC,
∴∠BPN=∠MPC,
∴△BPN≌△MPC,
∴PM=PB,PN=PC,
∵BP+PC=BC,
∴PM+PN=BC;
(2)BN=CM总成立,理由:
由(1)知△BPN≌△MPC,
∴BN=CM;
(3)解:如图③即为所求.
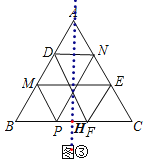
作ND∥BC交AB于N,作ME∥BC交AC于M,作EF∥AB交BC于F,连接DF,作直线AH⊥BC交BC于H,
同(1)可证△AND,△AME,△BPM,△CEF都是等边三角形,
∴D与N,M与E,B与C关于AH对称.
∴BM=CE,
∴BM=CF,
∴P与F关于AH对称,
∴所做图形是轴对称图形.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点(
经过点(![]() 1,0),对称轴为
1,0),对称轴为![]() .则下列结论:①
.则下列结论:①![]() ;②
;② ![]() ;③
;③![]() ; ④
; ④![]() .其中所有正确的结论是( )
.其中所有正确的结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() 分别是梯形
分别是梯形![]() 各边
各边![]() 、
、![]() 、
、![]() 、
、![]() 的中点.
的中点.
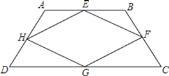
![]() 求证:四边形
求证:四边形![]() 平行四边形;
平行四边形;
![]() 当梯形
当梯形![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形;
是菱形;
![]() 在
在![]() 的条件下,梯形
的条件下,梯形![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
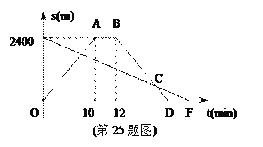
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() .将点
.将点![]() 绕着原点
绕着原点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到点
得到点![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ;再将点
;再将点![]() 绕着原点
绕着原点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到点
得到点![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ;…如此继续下去.
;…如此继续下去.
求:(1)点![]() 的坐标;(2)点
的坐标;(2)点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线![]() 图象的一部分,已知抛物线的对称轴是
图象的一部分,已知抛物线的对称轴是![]() ,与
,与![]() 轴的一个交点是
轴的一个交点是![]() ,有下列结论:
,有下列结论:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;
;
⑤点![]() ,
,![]() 都在抛物线上,则有
都在抛物线上,则有![]() .
.
其中正确的是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(﹣2,3),点B的坐标是(1,﹣1),连接AB,点C是坐标轴上任意一点,则使△ABC为等腰三角形的点C共有_____个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com