
(2013年广东梅州11分)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
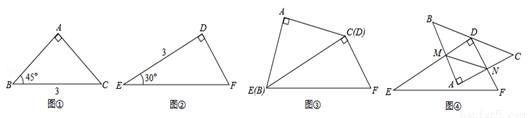
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.
探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
解:探究一:
(1)依题意画出图形,如答图1所示:

由题意,得∠CFB=60°,FP为角平分线,
则∠CFP=30°。
∴CF=BC•sin30°=3× =
= 。
。
∴CP=CF•tan∠CFP= ×
× =1。
=1。
过点A作AG⊥BC于点G,则AG= BC=
BC= ,
,
∴PG=CG﹣CP= ﹣1=
﹣1= 。
。
在Rt△APG中,由勾股定理得: 。
。
(2)由(1)可知,FC=
 .
.
如答图2所示,以点A为圆心,以FC= 长为半径画弧,与BC交于点P1、P2,则AP1=AP2=
长为半径画弧,与BC交于点P1、P2,则AP1=AP2= 。
。

过点A过AG⊥BC于点G,则AG= BC=
BC= ,
,
在Rt△AGP1中, ,∴∠P1AG=30°。
,∴∠P1AG=30°。
∴∠P1AB=45°﹣30°=15°。
同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°。
∴∠PAB的度数为15°或75°。
探究二:△AMN的周长存在有最小值。
如答图3所示,连接AD,

图3
∵△ABC为等腰直角三角形,点D为斜边BC的中点,
∴AD=CD,∠C=∠MAD=45°。
∵∠EDF=90°,∠ADC=90°,∴∠MDA=∠NDC。
∵在△AMD与△CND中, ,
,
∴△AMD≌△CND(ASA)。∴AM=CN。
设AM=x,则CN=x, ,
,
在Rt△AMN中,由勾股定理得:
 ,
,
∴△AMN的周长为:AM+AN+MN=
 。
。
当x= 时,有最小值,最小值为
时,有最小值,最小值为 。
。
∴△AMN周长的最小值为 。
。
【解析】探究一:(1)如答图1所示,过点A作AG⊥BC于点G,构造Rt△APG,利用勾股定理求出AP的长度。
(2)如答图2所示,符合条件的点P有两个.解直角三角形,利用特殊角的三角函数值求出角的度数。
探究二:如答图3所示,证明△AMD≌△CND,得AM=CN,则△AMN两直角边长度之和为定值;设AM=x,求出斜边MN的表达式,利用二次函数的性质求出MN的最小值,从而得到△AMN周长的最小值。
考点:几何变换综合题,单动点和旋转问题,角平分线的性质,锐角三角函数定义,特殊角的三角函数值,勾股定理,垂径定理,等腰直角三角形的性质,全等三角形的判定和性质,二次函数的性质。


科目:初中数学 来源:2013年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
(2013年广东梅州10分)如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.

(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
(2013年广东梅州8分)如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB与点E,且CF=AE,

(1)求证:四边形BECF是菱形;
(2)若四边形BECF为正方形,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
(2013年广东梅州8分)为建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如表:
|
|
单价(元/棵) |
成活率 |
植树费(元/棵) |
|
A |
20 |
90% |
5 |
|
B |
30 |
95% |
5 |
设购买A种树苗x棵,绿化村道的总费用为y元,解答下列问题:
(1)写出y(元)与x(棵)之间的函数关系式;
(2)若这批树苗种植后成活了925棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过31000元,则最多可购买B种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
(2013年广东梅州8分)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.

(1)求线段EC的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广东梅州卷)数学(解析版) 题型:解答题
(2013年广东梅州8分)已知,一次函数y=x+1的图象与反比例函数 的图象都经过点A(a,2).
的图象都经过点A(a,2).
(1)求a的值及反比例函数的表达式;
(2)判断点B 是否在该反比例函数的图象上,请说明理由.
是否在该反比例函数的图象上,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com