

| A. | ①②③ | B. | ②③ | C. | ①③④ | D. | ②④ |
分析 根据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各结论分析解答即可.
解答 解:根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/秒,
∴BC=BE=5,
∴AD=BE=5,故①正确;
∵从M到N的变化是2,
∴ED=2,
∴AE=AD-ED=5-2=3,
在Rt△ABE中,AB=$\sqrt{B{E}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴cos∠ABE=$\frac{AB}{BE}$=$\frac{4}{5}$,故②错误;
过点P作PF⊥BC于点F,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=$\frac{AB}{BE}$=$\frac{4}{5}$,
∴PF=PBsin∠PBF=$\frac{4}{5}$t,
∴当0<t≤5时,y=$\frac{1}{2}$BQ•PF=$\frac{1}{2}$t•$\frac{4}{5}$t=$\frac{2}{5}$t2,故③正确;
当t=$\frac{29}{4}$秒时,点P在CD上,此时,PD=$\frac{29}{4}$-BE-ED=$\frac{29}{4}$-5-2=$\frac{1}{4}$,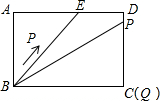
PQ=CD-PD=4-$\frac{1}{4}$=$\frac{15}{4}$,
∵$\frac{AB}{AE}$=$\frac{4}{3}$,$\frac{BQ}{PQ}$=$\frac{5}{\frac{15}{4}}$=$\frac{4}{3}$,
∴$\frac{AB}{AE}$=$\frac{BQ}{PQ}$,
又∵∠A=∠Q=90°,
∴△ABE∽△QBP,故④正确.
综上所述,正确的有①③④.
故选:C.
点评 本题考查了动点问题的函数图象,根据图(2)判断出点P到达点E时点Q到达点C是解题的关键,也是本题的突破口.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<5且x≠2 | B. | x≥5 | C. | x≤5且x≠-2 | D. | x≠-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.25×10-5 | B. | 2.5×10-5 | C. | 2.5×10-6 | D. | 25×10-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
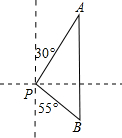 如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为(结果取整数,参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)( )
如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为(结果取整数,参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)( )| A. | 10海里 | B. | 11海里 | C. | 12海里 | D. | 13海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0或1 | B. | -2或0 | C. | -1或2 | D. | -2或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8000×108 | B. | 8×1010 | C. | 0.8×1011 | D. | 8×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
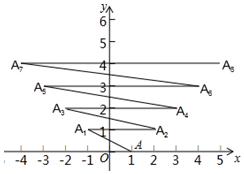 如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第102次跳动至点A102的坐标是( )
如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第102次跳动至点A102的坐标是( )| A. | (-50,50) | B. | (-51,51) | C. | (52,51) | D. | (51,50) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com