
分析 以AB为边的等边三角形,可求出该边上的高的长度,由于点C要落在二次函数的图象上,点C的纵坐标的绝对值即为AB边上的高的长度,从而可求出该点C的坐标.
解答 解:设AB边上的高为h,
∵等边△ABC的边长为2$\sqrt{3}$,
∴AB边上的高h=3,
设点C的纵坐标为y,
∵点C在二次函数的图象上,
∴|y|=3,
∴y=±3,
令y=3代入y=x2-2x-2,
解得:x=1±$\sqrt{6}$,
令y=-3代入y=x2-2x-2,
∴解得:x=1,
∴C的坐标为(1+$\sqrt{6}$,3)或(1-$\sqrt{6}$,3)或(1,-3)
故答案为:(1+$\sqrt{6}$,3)或(1-$\sqrt{6}$,3)或(1,-3)
点评 本题考查二次函数图象上的点特征,解题的关键是根据题意求出AB边上的高,从而得出C的纵坐标,本题属于中等题型.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
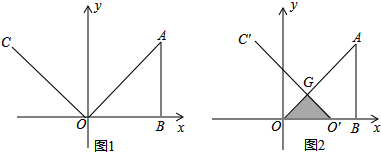
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
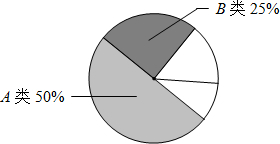 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | $\frac{1}{2}$ | |
| B类(60~79) | $\frac{1}{4}$ | |
| C类(40~59) | 8 | $\frac{1}{6}$ |
| D类(0~39) | 4 | $\frac{1}{12}$ |
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
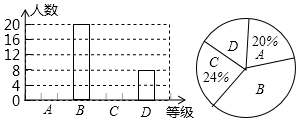 某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全).
某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全). | 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 等级 | A | B | C | D |
| 学生人数 | m | 20 | n | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
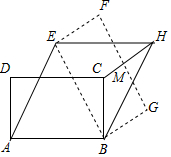 如图,矩形ABCD中,AB=3,AD=$\sqrt{3}$,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
如图,矩形ABCD中,AB=3,AD=$\sqrt{3}$,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
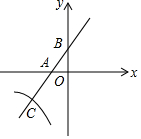 如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.
如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
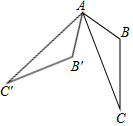 如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为( )
如图所示,△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为( )| A. | 33° | B. | 50° | C. | 17° | D. | 27° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
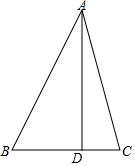 已知△ABC中,AD⊥BC于点D,∠BAC=45°,BD=6,CD=4,
已知△ABC中,AD⊥BC于点D,∠BAC=45°,BD=6,CD=4,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com